Математический аппарат Z-преобразования является основой теории дискретных САУ. Рассмотрим формулировки основных теорем Z-преобразования и примеры их применения.

1) Теорема о линейности преобразования:

Если , а α и β – константы, то

.

2) Теорема о смещении во временной области:

Если , а k – натуральное число, то

и

.

3) Теорема об умножении оригинала на экспоненту:

Если  и α – константа, то

.

4) Теорема о начальном значении:

Если  и существует предел , то

.

1) Теорема о конечном значении:

Если  и если функция  не имеет полюсов на окружности единичного радиуса  и вне ее на комплексной плоскости Z, то

.

Пример 7

Необходимо найти Z-изображение функции .

На основании теоремы линейности можно записать:

.

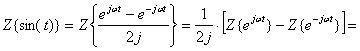
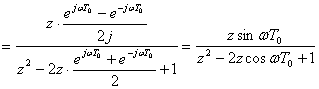Пример 8

Необходимо найти Z-изображение функции .

Используя теорему об умножении на экспоненту применительно к выражению (2.6), можно записать:

;

.
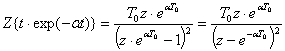