Рассматривается два способа решения задачи отделения корней – графический и аналитический.

Существует два подхода к графическому отделению корней.

1. Строится график:  и приблизительно находятся абсциссы точек пересечения графика  с осью x (рис. 2.1).

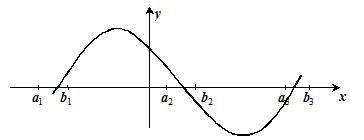
Рис. 2.1. Графическое отделение корней

2. Сначала уравнение  записывается в виде , а затем строятся графики:  и приблизительно находятся абсциссы точек пересечения этих графиков (рис. 2.2).

Пример

Требуется отделить корни уравнения: .

Решение. Запишем уравнение в виде: , то есть , , и построим графики:  (рис. 2.3). Абсцисса точки пересечения графиков принадлежит отрезку [0, 1].

Отрезок  [0, 1]  содержит один корень уравнения: .

Аналитически корни уравнения  можно отделить, используя свойства функции, например, опираясь на следующую теорему.

Теорема

Рис. 2.2. Графическое отделение корней

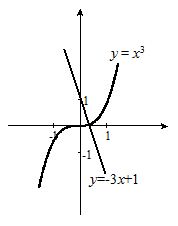
Рис. 2.3. Отделение корня

Если f(x) = 0 является непрерывно дифференцируемой функцией на отрезке , первая производная f не меняет знак на [a, b] , и на концах отрезка функция f принимает значения разных знаков , то внутри отрезка [a, b] содержится один корень уравнения f(x) = 0.

Отметим, что в дальнейшем мы будем для пространства n раз непрерывно дифференцируемых функций на отрезке [a, b] использовать обозначение: . Если функция f является непрерывной функцией на отрезке [a, b], то это можно записать так: . Если функция f является непрерывно дифференцируемой на отрезке [a, b], то это можно записать следующим образом: . Если f – дважды непрерывно дифференцируемая функция на отрезке [a, b], то будем использовать обозначение:  и т.д.