Чтобы из бесчисленного количества вариантов температурных полей, выделить поле, интересующее нас в конкретном случае, необходимо оговорить и математически описать те частные особенности, которые характеризуют именно этот вариант процесса теплопроводности. Частные особенности, дающие совместно с дифференциальным уравнением теплопроводности полное математическое описание процесса теплообмена в конкретной задаче, называют условиями однозначности, В этих условиях должны быть оговорены:
1) форма, размеры и теплофизические характеристики тела (системы тел), в котором происходит процесс передачи теплоты;
2) форма, распределение плотности теплового потока и другие характеристики источников или стоков, действующих в рассматриваемом процессе;
3) распределение температур в рассматриваемой системе тел до того, как начался изучаемый процесс (так называемые начальные условия);
4) условия теплообмена на поверхностях тела, соприкасающихся с окружающей средой или с другими телами, входящими в систему (так называемые граничные условия).
Выполняя математическое описание условий однозначности при решении конкретных практических задач, в том числе и задач, относящихся к технологическим подсистемам, обычно прибегают к той или иной схематизации процесса теплообмена. Это значит, что фактические тела и источники, действующие в реальном процессе, заменяют телами и источниками более простой формы, приближенно описывающими оригиналы. Фактические условия взаимодействия тел с окружающей средой и начальные условия также схематизируют, заменяя сложные ситуации, имеющие место в действительности, более простыми, идеализированными.
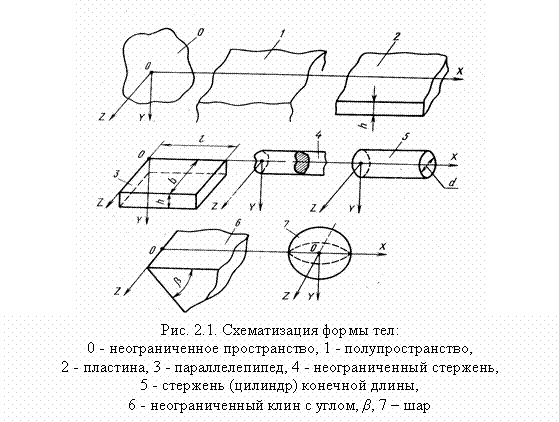
Схематизация формы нагретого тела делается с целью облегчения математического описания процесса теплообмена в конкретных задачах рис. 2.1.
Пример преобразования сложной формы тела в более простую при схематизации процесса шлифования кулачка показан на рис. 2.2.
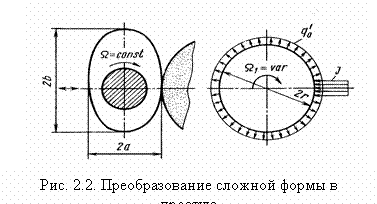
Если в процессе шлифования плотность стока теплоты в окружающую среду (охлаждающую жидкость) с поверхности кулачка равна qо, Вт/м2, то в расчетной схеме должно фигурировать скорректированное значение q’о = Pqо/ (2πr), где P — периметр эллипса.