Сочетанием  элементов множества X называется подмножество конечного множества A Í X. Если |A| = k,  |X| = n, то подмножество X называется сочетанием из n по k. Например, сочетания трех цветов семицветной радуги будут описываться подмножествами, состоящими из трех элементов выбранных из множества, состоящего из 7 элементов.

Треугольник Паскаля и бином Ньютона

Для вычисления числа сочетаний построим таблицу, которая называется треугольником Паскаля. Она основана на следующей теореме:

Теорема 1

Число сочетаний удовлетворяет соотношениям:

;                       (при 0 < k < n).

Доказательство

Число пустых подмножеств равно 1. Стало быть, . Подмножества, состоящие из n элементов, совпадают со всем множеством, отсюда . Число сочетаний, не содержащих n-й элемент, равно , а число сочетаний, содержащих n-й элемент, равно . Следовательно, при 0 < k < n:

Таблица 2.1 строится на основе теоремы 1 и называется треугольником Паскаля.

Таблица 2.1 Треугольник Паскаля

n k	0	1	2	3	4	5
0	1
1	1	1
2	1	2	1
3	1	3	3	1
4	1	4	6	4	1
5	1	5	10	10	5	1
6	1	6	15	20	15	6

Теорема 2

Число сочетаний из n по k равно:

.

Доказательство

Применим метод индукции по n. При n = 0 и k = 0 получаем:

.

Пусть теорема верна для n. С помощью теоремы 1 получаем:

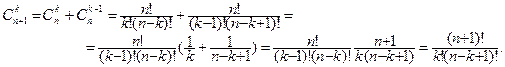
Откуда формула верна для n + 1 и всех k < n + 1.

Другой способ доказательства заключается в сопоставлении каждой инъекции ее образа. В этом случае, учитывая, что число инъекций с одинаковым образом равно k!, получаем:

 Þ 

Теорема 3

  (бином Ньютона).

Доказательство

Применим метод индукции по n. Пусть формула верна для n. Тогда

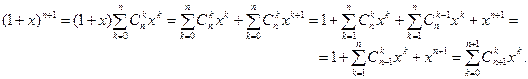
Можно предложить также другое доказательство. Рассмотрим произведение n сомножителей:

(1 + x) (1 + x) … (1 + x).

Сомножители будем рассматривать как ящики. Произведение равно сумме степеней x^k, причем при каждом k слагаемые x^k получаются выбором из ящиков k элементов, равных x. Отсюда коэффициент при x^k  будет равен количеству содержащих k элементов подмножеств множества, состоящего из n элементов.

Применение сочетаний

Сочетание можно интерпретировать как размещение без повторений неразличимых предметов в ящиках.

Пример 1

Найдем вероятность угадать 7 номеров из 49 (игра спортлото). Количество вариантов равно числу сочетаний  из 49 элементов по 7. Существует единственный благоприятный вариант. Отсюда вероятность равна:

.

Теорема 4

Число возрастающих функций  f: {1, 2,…, k} ® {1,2, …, n} равно .

Доказательство

Каждой возрастающей функции сопоставим ее образ:

{f(1),  f(2), …, f(k)} Í {1,2, …, n}.

Получим биекцию между возрастающими функциями и подмножествами множества {1, …, n}, состоящими из k элементов. Согласно определению сочетания, число таких подмножеств равно числу сочетаний .

Замечание

Возрастающая функция задается возрастающей последовательностью k чисел. Отсюда число возрастающих последовательностей x₁ < …<x_k  чисел, принадлежащих множеству {1, 2, …, n}, будет равно .

Теорема 5

Число последовательностей натуральных чисел (x₁, x₂, …, x_k),  x_i³1, удовлетворяющих уравнению

x₁ +  x₂  + …  + x_k = n,

равно .

Доказательство

Каждой последовательности (x₁, x₂, …, x_k), удовлетворяющей данному уравнению, сопоставим возрастающую последовательность:

y₁ = x_1, y₂ = x₁ + x₂, …,  y_k-1 = x₁ + x₂ +…+ x_k-1.

Наоборот, каждой возрастающей последовательности y₁ < …< y_k-1 < n можно сопоставить решение данного уравнения, состоящее из чисел:

x₁ = y₁, x₂ = y_{2 –} y₁, …, x_k-1 = y_{k-1 –} y_k-2, x_k = n – y_k-1.

Получаем биекцию между решениями данного уравнения и возрастающими последовательностями, состоящими из k-1 чисел, принимающих значения 1, 2, …, n – 1. По теореме 4 число таких возрастающих последовательностей равно .

Теорема 6

Число неубывающих сюръекций {0,1, …, n –1} ® {0, 1, …, k – 1} равно .

Доказательство

Каждая сюръекция задает разбиение множества  {0, 1, …, k – 1} на подмножества f ^-1(0), f ^-1(1), …, f ^─1(n  – 1). Пусть  m₀ – наибольший в  f ^-1(0),  m₁ – наибольший в  f ^-1(1), … , m_n-2 –  наибольший в  f^-1(n – 2). Тогда   m_n-1 = k  – 1.  Следовательно,

0 ≤ m₀ < m₁ < … <  m_n-2  ≤ k – 2.

Число таких последовательностей равно   –  количеству возрастающих функций n – 1 ® k – 1.

Пример 2

Число неубывающих сюръекций n ® 1 равно .

Число неубывающих сюръекций 3 ® 2 равно .

Сочетания с повторениями

Сочетанием с повторением из множества {e_1, e_2, …, e_n} называется линейная комбинация  x₁e₁  + x₂e₂  + …+x_n e_n, состоящая из x₁  элементов e₁, из x₂   элементов e₂,… из x_n   элементов e_n , где x_i   ≥ 0 – неотрицательные целые числа. Если  x₁  + ×…+x_n = k, то оно называется сочетанием с повторениями из n по k.

Пусть, например, имеется 3 цвета: красный, зеленый, синий. Интенсивности этих цветов равны. Сколько смесей суммарной интенсивности 10 можно получить, смешивая  x₁   красных, x₂  зеленых и x₃  синих цвета?

Лемма 1

Пусть   – число сочетаний с повторениями из n по k. Тогда  равно числу неубывающих функций:

{1,2, …, n-1} ® {0,1,2, …, n}.

Доказательство

Рис. 2.2.  Решение уравнения x₁ + ××× +x_n = k

Каждому решению  x₁  + …+x_n = k соответствует неубывающая последовательность:

y₁ ≤ y₂ ≤  … ≤ y_n-1,

где y₁ = x₁, y₂ = y₁+x₂, …, y_n-1 = y_n-2 + x_n-1.

Теорема 7

.

Доказательство

Рассмотрим график неубывающей функции (рис. 2.3). График задается последовательностью из 0 и 1

0 0 1 1 0 0 … 0 1 0 0 … 1 1 … 1,

состоящей из n – 1 + k разрядов, имеющих k единиц.

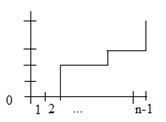
Рис. 2.3. График неубывающей  функции

Следствие 1

Число сочетаний с повторениями  равно числу неубывающих функций:

{1,2, …, k} ® {1,2, …, n}.

Доказательство

Первый способ: транспонировать графики. Если график (см. рис.2.3) отразить относительно прямой y = x, то получим график функции {1,2, …, k} ® {1,2, …, n}. Это доказывает утверждение следствия.

Второй способ: число неубывающих функций {1,2, …, k} ® {1,2, …, n} равно:

= =.

Получаем следующую таблицу 2.2, содержащую числа конфигураций

Таблица 2.2 Число конфигураций

	функций m®n	неубывающих функций m®n
Всех	nm
Инъективных
Сюръективных	?
Биективных	n!, если m = n, иначе 0	1, если m = n, иначе 0

В таблице 2.2  m = {0,1, …, m – 1}. Например, число неубывающих сюръективных отображений  {0,1, …, m-1} ® {0,1, …, n – 1} равно .