Пусть дана клауза в своей наиболее общей форме:

В₁, В₂, …, В_n Þ А₁, А₂, …,A_n

Шаг 1. Снятие отрицаний с посылок и заключений. С этой целью нужно опустить знак отрицаний у A_i и B_j и перенести их в противоположные стороны относительно символа Þ.

Шаг 2. Если слева от символа   встречается конъюнкция, а справа дизъюнкция, то их следует заменить на запятые.

Шаг 3. Если после предыдущих шагов оказалось, что связкой, расположенной слева от Þ, является дизъюнкция, а справа – конъюнкция, то образуются две новые клаузы, каждая из которых содержит одну из двух подформул, заменяющих исходную клаузу.

Шаг 4. Если одна и та же буква находится с обеих сторон символа, то такая строка считается доказанной. Исходная клауза является теоремой, если все ветви оканчиваются истинными клаузами. В противном случае переходим к шагу 3.

Пример 53.

Выяснить, является ли клауза теоремой:

.

Решение.

Шаг 1. .

Избавляемся от отрицаний. В результате получаем: .

Шаг 2. Поскольку  слева от символа Þ  не встречается конъюнкция, а справа не встречается дизъюнкция, то шаг 2 как таковой отсутствует.

Шаг 3. Построим дерево доказательств (рис. 2.1):

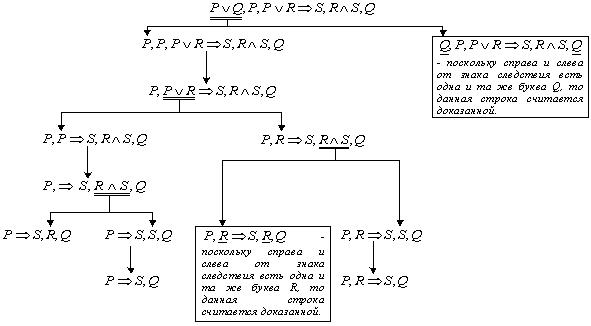
Рис. 2.1. Дерево доказательств для примера 53

Так как есть не доказанные строки, то исходная клауза теоремой не является.

Пример 54.

Выяснить, является ли клауза теоремой:

.

Решение.

Представим ход доказательства в виде дерева (рис. 2.2). Поскольку все строки доказаны, то исходная клауза является теоремой.

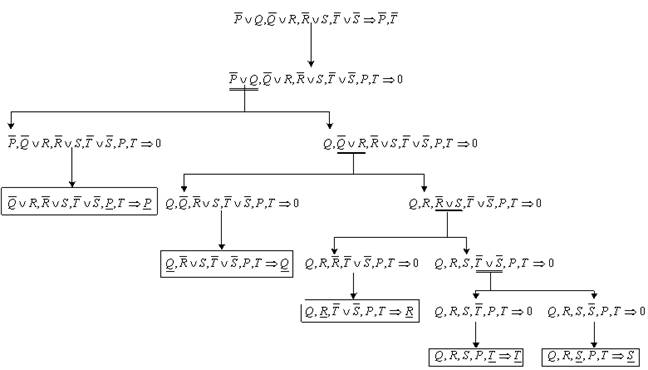
Рис. 2.2. Дерево доказательств для примера 54