В тавровых соединениях элементы соединения располагаются во взаимно перпендикулярных плоскостях. Соединение выполняют с разделкой кромок стыковым швом (рис. 2.14, а). В данном случае расчет на прочность ведут по нормальным напряжениям σ (рис. 2.14, в). При совместном действии силы (F) и момента (M)  условие прочности имеет вид:

.

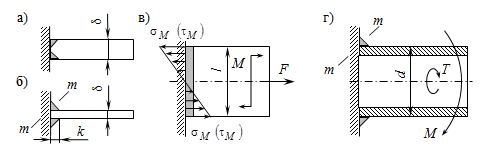
Рис. 2.14. Тавровые соединения

При выполнении соединения без разделки кромок угловыми швами (рис. 2.14, б) расчет на прочность ведут по касательным напряжениям τ (рис. 2.14, в). При совместном действии силы (F)  и момента (M)   условие прочности имеет вид:

.

Для таврового соединения трубы, нагруженного изгибающим (M)  и крутящим (T) моментами (рис. 2.14, г), напряжение в шве от крутящего момента определяется по формуле:

,   (2. 11)

где  – окружная сила на среднем диаметре  кольцевой площадки;  – площадь кольцевой площадки.

В формуле (2.11) принято, что катет шва (k) мал по сравнению с диаметром трубы (d). При этом считают, что напряжения от крутящего момента  распределены равномерно по кольцевой площадке разрушения шва, а средний диаметр этой площадки равен:

.

Напряжение в шве от изгибающего момента  определяется следующим образом:

.  (2.12)

В формуле (2.12) учтено, что осевой момент сопротивления (W) в два раза меньше полярного момента сопротивления (W_р) Напряжения  и   в сечении   (рис. 2.14, г) взаимно перпендикуляры. Поэтому суммарное напряжение равно:

.