В настоящее время существует большое количество разнообразных методов прогнозирования. Эти методы различаются по назначению, по виду используемой в них информации, по реализуемым формальным процедурам получения численных оценок параметров прогнозных моделей, по периоду упреждения и т.д. Предпринимаются попытки связывать методы прогнозирования с самими прогнозируемыми объектами. Отсюда появились методы экономического прогнозирования, социального прогнозирования, научно-технического прогнозирования и т.д.
Действительно, в ряде случаев существует определенная специфика описания поведения тех или иных объектов. Так, процессы развития технических систем описываются моделями, существенно отличными от моделей, скажем, демографических процессов. Вместе с тем, в огромном большинстве случаев непосредственно прогнозирование понимается как способ получения будущих значений процессов, обладающих определенной динамикой. Поэтому важнейшим классом методов получения прогнозных результатов является прогнозирование временных рядов, т.е. процессов, представленных упорядоченной во времени последовательностью наблюдений.
Различие исходной информации требует выбора адекватного метода прогнозирования. При этом оценка специфики информации об объекте носит как качественный, так и количественный характер. Так, если с помощью статистических тестов установлено наличие переменных составляющих, то выбираются спектральные методы или адаптивные с учетом сезонности. При существенной автокорреляции используются методы авторегрессии. При наличии некоторых отклонений от нормального закона распределения выборки применяются робастные (нечувствительные к малым изменениям) процедуры оценивания и т.д.
Для получения прогнозных результатов широкое применение имеют методы так называемого «многофакторного прогнозирования». Эти методы отличает простота реализации, достаточно «мягкие» требования к исходной информации, возможность получить достоверные прогнозные результаты как для относительно сложной динамики развития исследуемой системы, так и для сложной организации самой системы, т.е. при сложном характере связей между зависимой и независимой переменными. Процедурные преимущества методов (достаточная простота процедуры получения численных значений параметров моделей) вместе с тем предполагают четкий выбор вида функциональной зависимости, объясняющей зависимость переменной от времени и независимых переменных. Строго обоснованных формальных процедур по выбору функциональной зависимости не существует, и здесь главную роль играют интуиция и опыт прогнозиста.
С точки зрения выбора вида функциональной зависимости методы многофакторного прогнозирования не уступают другим методам прогнозирования, в которых выбор констант, параметров или вида функциональной зависимости не базируется на каких-либо формальных предпосылках.
Качество получаемых прогнозных результатов, таким образом, зависит, прежде всего, от правильности выбора вида функциональной зависимости и уже в меньшей степени от качества исходной информации.
Исходной информацией для получения прогнозных результатов с помощью методов многофакторного прогнозирования является матрица наблюдений по времени зависимой и независимых переменных, т.е.
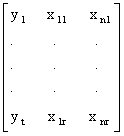 ,
,
где yt – значение зависимой переменной, xit – t-e значение i-й независимой переменной.
Каждый столбец матрицы исходной информации представляется временным рядом наблюдений, упорядоченных во времени.
Для исходной информации должны быть выполнены некоторые основные предпосылки, такие, как
T ³ (3…5)n; T ³ 15…20.
Это означает, что количество наблюдений по каждому фактору должно быть в 3—5 раз больше числа исследуемых факторов, но во всяком случае не менее 15 – 20 наблюдений. Более детальный анализ исходной информации проводится на основании статистических критериев.
Использование в качестве исходной информации временных рядов по совокупности показателей, включаемых в модели, предполагает применение методов прогнозирования одномерных временных рядов для получения будущих значений каждой из зависимых переменных. Методологической процедурной основой определения оценок прогнозных моделей в случае, когда информация представлена в виде временных (динамических) рядов наблюдений, является метод наименьших квадратов.
В общем случае задача получения прогнозной модели может быть сформулирована следующим образом: построить некоторую зависимость
yt = f (z1,…,zn, t, q1, q2, …, qn, qn+1, et),
где z1,…,zn – набор переменных, описывающих объект; t – время; q1,…,qn, qn+1 – некоторые параметры; et – случайная ошибка.
Другим методом статистического прогнозирования является выделение функционально однородных интервалов, внутри которых информацию можно считать однородной по определенным признакам. И для этих интервалов следует экспертным путем выбирать соответствующие веса.
Существует несколько критериев для определения оценок моделей. Соответствующими им методами получения оценок коэффициентов прогнозных моделей являются процедуры, основанные на минимизации не суммы квадратов рассогласований реальных и модельных значений, а минимизации суммы модулей рассогласований:
![]()
или минимизации максимума модуля рассогласования:
Ф = max |![]() – yt| ® min.
– yt| ® min.