Значительная часть экономических задач, относящихся к задачам ЛП, требует целочисленного решения. К ним относятся задачи, у которых переменные величины означают количество единиц неделимой продукции, например, распределение производственных заданий между предприятиями; раскрой материалов, загрузка оборудования, распределение судов по линиям, самолетов по рейсам, а также задачи по производству неделимой продукции.
Если единица составляет малую часть всего объема производства, то оптимальное решение находят обычным симплексным методом, округляя его до целых единиц, исходя из смысла задачи. В противном случае округление может привести к решению, далекому от оптимального целочисленного решения.
Постановка задачи
Задача целочисленного программирования (ЦП) формулируется также как и задача ЛП, но включается дополнительное требование, состоящее в том, что значения переменных, составляющих оптимальное решение, должны быть целыми неотрицательными числами.
Если этому требованию должны удовлетворять все искомые переменные, то получаем полностью целочисленную задачу ЛП, если же этому требованию должны удовлетворять только некоторые из переменных, то получаем частично целочисленную задачу ЛП. Модель целочисленной задачи ЛП имеет вид:

Графический метод
Полностью (или частично) целочисленную задачу с двумя переменными можно решить графически, учитывая, что допустимое множество решений этой задачи состоит из совокупности изолированных целочисленных точек (точки целочисленной координатной сетки), принадлежащих множеству решений задачи ЛП без дополнительного требования целочисленности (рис. 2.19).
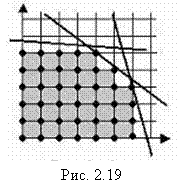 Таким образом, наложение требования целочисленности, приводит нас к новой задаче ЛП со следующими свойствами:
Таким образом, наложение требования целочисленности, приводит нас к новой задаче ЛП со следующими свойствами:
· новый многогранник решений содержит все целые точки, заключавшиеся в первоначальном многограннике решений;
· новый многогранник решений не является выпуклым;
· любая его угловая точка является целой;
· так как целевая функция достигает оптимума в угловой точке многоугольника решений, то построением такого многоугольника и обеспечивается целочисленность оптимального решения.