Перечисление элементов объединения подмножеств

Обобщим формулу:

|A₁È A₂| = |A₁ | + |A₂| — |A₁Ç A₂|.

Эта формула имеет многочисленные приложения. Мы применим ее для решения задачи о встречах, задачи о счастливых билетах и для нахождения значений функции Эйлера j(n). 

Теорема 1 (формула включения-исключения)

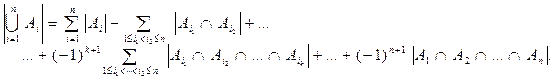
Доказательство

Применим метод индукции. При n = 1, 2 утверждение очевидно. Заметим, что имеет место соотношение:

.

Предположим, что для n  множеств утверждение верно. Докажем ее для n + 1. Имеем по формуле включения-исключения для n множеств A₁ÇA_n+1,  A₂ÇA_n+1, …,  A_nÇA_n+1:

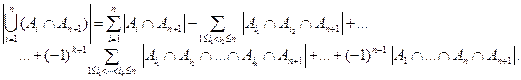
Поскольку формула верна при n = 2, то справедливо равенство:

.

Отсюда мы видим, что  содержит слагаемое, равное сумме  и соответствующее первому слагаемому в формуле включения-исключения для n + 1 множеств. Объединим k-е слагаемое, определенное в формуле для , и (k – 1)-е слагаемое в формуле включения-исключения для  . В силу

 =

 будем иметь:

-=

=.

В результате мы получили k-е слагаемое в формуле включения-исключения для множеств A₁, …, A_n+1. Следовательно, эта формула верна для n+1 множеств. Что и требовалось доказать.

Задача о встречах

В дождливую погоду n человек пришли в театр. Они сдают зонтики в гардероб. После окончания спектакля получают зонтики обратно в случайном порядке. Какова вероятность того, что каждый из них получит чужой зонтик?

Задача сводится к нахождению числа перестановок элементов множества {1, 2, … ∙, n}, не имеющих неподвижных точек.

Пусть S_i состоит из перестановок,  оставляющих неподвижной точку i.  Вычислим:

| S₁È S₂ È …∙È S_n|.

Искомая вероятность будет равна:

;

Получаем:

.

Отсюда число перестановок, не имеющих неподвижных точек, равно:

.

Искомая вероятность равна:

.

Число f(n) будет ближайшим к дроби     целым числом. При n®¥ вероятность стремится к .

Задача о счастливых билетах

Требуется найти число решений уравнения:

x₁ + x₂ + x₃ = y₁ + y₂ + y₃,

где  0 £  x_i, y_i  £ 9.

Решение

Подстановка x₄ = 9 - y_1, x₅ = 9 - y_2, x₆ = 9 - y₃  устанавливает биекцию между решениями этого уравнения и уравнения:

x₁ + x₂ + x₃ + x₄ + x₅ + x₆ = 27,

где  0 £ x_i £ 9.

Найдем число разложений:

x₁ + x₂ + x₃ + x₄ + x₅ + x₆ = 27,

где  0£ x_i £9.

Пусть  U₁ –  число разложений с x₁ ³ 10;    U₂ –  число разложений с x₂ ³ 10,   U₆ –  число разложений с x₆ ³ 10. Тогда

| U_i ÇU_jÇU_k | = 0      при |{i,j,k}| = 3.

Вычислим число разложений, не удовлетворяющих неравенствам 0£ x_i £9. Оно равно:

| U₁ ÈU₂ÈU₃ ÈU₄ ÈU₅ ÈU₆ | = 6|U₁| – 15|U₁ÇU₂|,

где | U₁| – число решений уравнения

(x_{1 –} 10) + x₂ + x₃ + x₄ + x₅ + x₆ = 27 – 10,

а |U₁ÇU₂| – число решений уравнения

(x_{1 –} 10)+(x₂ – 10) + x₃ + x₄ + x₅ + x₆ = 27 – 10 – 10.

Получаем:

| U₁ ÈU₂ÈU₃ ÈU₄ ÈU₅ ÈU₆ | = .

Из числа всех разложений вычитаем разложения с x_i ≥ 10. Получаем окончательный ответ:

.

Функция Эйлера

Пусть n – положительное натуральное число, j(n) – количество натуральных чисел 0< d £ n, взаимно простых c n (т.е. не имеющих одинаковых делителей, кроме 1). Например, при n = 10, dÎ{1, 3, 7, 9}  и  j(10) = 4. Функция j(n) называется функцией Эйлера.

Теорема 2

,

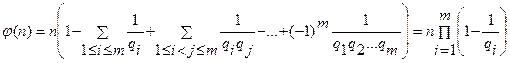где q₁, …, q_т  являются различными простыми делителями числа n.

Доказательство

Находим числа, не взаимно простые с n, по формуле включения и исключения, пользуясь тем, что количество делящихся среди {1,2, …, n} на число q равно n/q. Затем это число отнимаем от n.