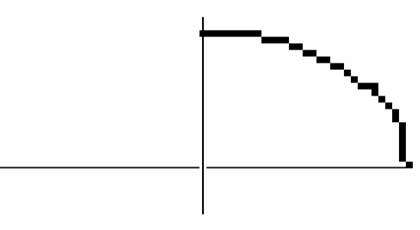
Метод приращений – это метод генерации точек на экране компьютера, близких к кривой, заданной уравнением f(x,y)=0. Этот метод был предложен в 60-е годы двадцатого века, для генерации точек окружности, а затем был обобщен на кривые второго порядка. В пп. 2.2 мы рассматривали частный случай этого метода, применяемый для генерации точек отрезка прямой. В дальнейшем полагаем, что нам задано уравнение кривой f(x,y)=0. В качестве начальной точки (x₀,y₀) выбирается точка, принадлежащая кривой. Все точки области, содержащей достаточно гладкую кривую f(x,y) можно разбить на три множества: множество точек принадлежащих кривой (для этих точек выполняется условие f(x,y)=0), множество точек области, для которых выполняется условие f(x,y)>0 и множество точек, для которых выполняется условие f(x,y)<0 (рис. 10).

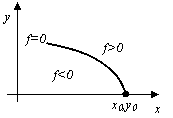Рис. 10. Метод приращений

В дальнейшем будем руководствоваться следующим правилом. Если методом приращений найдена некоторая точка (x_i,y_i), причем f(x_i,y_i)<0, то для того, чтобы сгенерированная последовательность точек была близка к идеальной кривой, будем стремиться перейти в такую точку (x_i+1,y_i+1), для которой выполняется условие f(x_i+1,y_i+1)>0, и наоборот. Другими словами, если мы выставили точку слева от кривой, то мы стремимся перейти на правую сторону от кривой и наоборот.

Опишем метод подробнее. Выбираем начальную точку (x₀,y₀), принадлежащую кривой, и направление движения вдоль кривой. Затем разобьем кривую на отрезки кривой, причем для каждого отрезка будет выполняться следующее условие: вектор касательной для всех точек отрезка кривой принадлежит только одной октанте (октанта – это одна восьмая часть плоскости, на рис. 11 приведена нумерация октант). Например, все точки эллипса, принадлежащие первой четверти, разобьются на два отрезка. Для первого отрезка вектор касательной V принадлежит третьей октанте, а для второго отрезка вектор касательной V₁ принадлежит четвертой октанте (рис. 12).

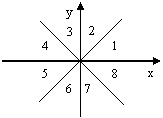
Рис. 11. Нумерация октант

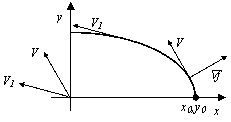
Рис. 12. Генерация точек эллипса

Зная уравнение кривой, мы можем найти вектор касательной и определить номер октанты. Для этого сначала запишем градиент

.

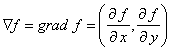Вектор касательной перпендикулярен градиенту (рис. 12). Любому вектору а=(а_х,а_у) на плоскости ОХУ перпендикулярны два вектора: вектор b₁=(-a_y,a_x) и вектор b₂=(a_y,-a_x). Следовательно, градиенту перпендикулярны два вектора

.

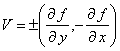Нужный нам вектор определяется, исходя из направления движения вдоль кривой.

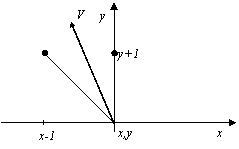Рис. 13. Перемещения

Генерацию точек кривой будем производить следующим образом: сначала выведем все точки, принадлежащие первому отрезку кривой, затем второму и т. д. Например, для генерации точек эллипса, принадлежащих первой четверти, требуется вывести два отрезка кривой (рис. 12).

Для всех точек каждого отрезка кривой вектор касательной принадлежит только одной октанте. А зная, какой октанте принадлежит вектор касательной, определим в какие две точки возможно перемещение. Например, если вектор касательной принадлежит третьей октанте (рис. 13), то из точки (х,у) мы можем перейти либо в точку (х,у+1), либо в точку (х-1,у+1).

А для того, чтобы из этих двух возможных точек выбрать одну, воспользуемся сформулированным ранее правилом. То есть из текущей точки (х_i,у_i) мы можем перейти либо в точку (х_j,у_j), либо в точку (х_k,у_k), причем f(х_j,у_j)?f(х_k,у_k)<0. Пусть f(х_j,у_j)>0, а f(х_k,у_k)<0. В этом случае поступаем следующим образом: если f(х_i,у_i)<0, то переходим в точку (х_j,у_j), и наоборот, если f(х_i,у_i)?0, то переходим в точку (х_k,у_k).

Для уменьшения времени работы программы в дальнейшем, вместо значения f(х_i,у_i) будем вычислять значение величины d_i, причем d_i=f(х_i,у_i). Так как начальная точка (х₀,у₀) принадлежит кривой, то d₀=f(х₀,у₀)=0. Величина d_i вычисляется по формуле

d_i=d_i-1+f(х_i,у_i)-f(х_i-1,у_i-1).

В дальнейшем мы будем вычислять приращение функции f(х,у): f(х_i,у_i)- f(х_i-1,у_i-1).

Пример генерации точек эллипса, принадлежащих первой четверти. Уравнение эллипса х²/а²+у²/b²=1 запишем в виде f(х,у)=b²x²+a²y²-a²b²=0. В качестве начальной точки (х₀,у₀) рекомендуется выбирать точку кривой, принадлежащей оси координат. В нашем случае, в качестве начальной точки можно выбрать точку (а,0) или (0,b). Выбираем точку х₀=а, у₀=0. Направление движения вдоль кривой – против часовой стрелки. Мы уже отмечали (рис. 12), что, в этом случае, сначала выводится отрезок кривой, для которого вектор касательной принадлежит третьей октанте, а затем отрезок, для которого вектор касательной принадлежит четвертой октанте.

Запишем градиент функции f

.

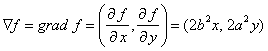Вектор касательной равен либо V=(-2a²y,2b²x), либо w=(2a²y,-2b²x). Вектор w=(w_x,w_y) принадлежит седьмой октанте (рис. 11), так как w_x>0, а w_y<0. Вектор V=(v_x,v_y) принадлежит третьей октанте (рис. 12), так как V_x<0, a V_y>0. Следовательно, вектор касательной V=(-2a²y,2b²x).

Запишем условие, при выполнении которого, вектор касательной принадлежит третьей октанте: ½V_y½>½V_x½, в нашем случае: ½2b²x½>½-2a²y½. Учитывая, что x>0 и y>0, так как они принадлежат первой четверти, получаем условие b²x>a²y. Если  вектор касательной принадлежит третьей октанте (рис. 13), то возможны два перемещения

Отметим, что у этих двух перемещений у координата одинакова, следовательно, не зависимо от того в какую точку мы будем перемещаться, у увеличится на 1.

Вычислим соответствующие приращения функции f(х,у)

f(х_i,у_i+1)- f(х,у)               =b²x²+a²(y+1)²-a²b²-b²x²-a²y²+a²b²=a²(2y+1)>0,

f(х-1,у+1)- f(х,у)=b²(x-1)²+a²(y+1)²-a²b²-b²x²-a²y²+a²b²=b²(-2x+1)+a²(2y+1)<0.

Первое приращение положительно, так как y>0, а второе приращение отрицательно, так как b²x>a²x для этого отрезка кривой.

Обозначим a² через a2 и b² через b2, запишем алгоритм:

a2=a², b2=b², x=a, y=0, delta=0       //входные параметры

while (b2*x>a2*y)      //пока вектор касательной принадлежит третьей октанте

  point(x,y)                                            //ставим точку с координатами (x,y)

  if (delta<0)

              delta=delta+a2*(y*2+1)       //положительное приращение

  else

              delta=delta+a2*(y*2+1)+b2(-x*2+1)         //отрицательное приращение

              x=x-1                                     //          x уменьшается на 1

  end if_else

  y=y+1                                                //          y увеличивается на 1

end while

Для второго отрезка эллипса вектор касательной V принадлежит четвертой октанте. В этом случае (рис. 14) выполняется условие ½V_y½<½V_x½ и V_y³0.

Первое условие после выполнения цикла while (b2*x>a2*y) выполнено, следовательно, второе условие (V_y³0) определяет принадлежность вектора V к четвертой октанте. Точнее, выполнение этого условия, гарантирует, что вектор касательной принадлежит четвертой, а не пятой октанте. Так как V_y=2b²x, то это условие запишется следующим образом: 2b²x³0, упрощая, получим: x³0. Так как вектор касательной принадлежит четвертой октанте (рис. 14), то возможны перемещения

У этих двух перемещений x координата одинакова, следовательно, x уменьшается на 1, независимо от того в какую точку мы будем перемещаться.

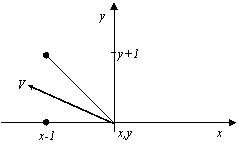Рис. 14. Перемещения

Вычислим соответствующие приращения функции f(x,y).          

f(х-1,у+1)=b²(-2x+1)+a²(2y+1)>0,

f(х-1,у)- f(х,у)=b²(x-1)²+a²y²-a²b²-b²x²-a²y²+a²b²=b²(-2x+1)<0.

Первое приращение положительно, так как b²x<a²y для этого отрезка кривой, а второе приращение отрицательно, так как x³0.

Запишем алгоритм:

while (x³0)                                //пока вектор касательной в четвертой октанте

  point(x,y)                                            //ставим точку с координатами (x,y)

  if (delta³0)

              delta=delta+b2*(-x*2+1)     //отрицательное приращение

  else

              delta=delta+b2*(-x*2+1)+a2(y*2+1)         //положительное приращение

              y=y+1                                    //y увеличивается на 1

  end if_else

  x=x-1                                                 //x уменьшается на 1

end while

Приведем пример текста программы и результаты ее работы для случая, когда элементом изображения является заполненный прямоугольник, построенный с помощью функции bar.

Программа

#include <stdio.h>

#include <graphics.h>

#include <conio.h>

int x0, y0; //экранные координаты начала координат

int hx, hy; //половины ширины и высоты пиксела

void point(int ix, int iy)

{bar (x0+hx*2*ix-hx+1, y0-hy*2*iy-hy+1, x0+hx*2*ix+hx-1, y0-hy*2*iy+hy-1);}

main()

{

int gdriver = DETECT, gmode;

int x, y, a=30, b=20;

float delta;

long a2, b2;

hx=3; hy=3;

//Инициализация графического режима

initgraph ( &gdriver, &gmode, "D:\BC\BGI") ;

x0 = getmaxx()/2; y0 = getmaxy()/2;

moveto(0,y0); linerel(getmaxx(),0);

moveto(x0,0); linerel(0, getmaxy());

a2=a*a; b2=b*b;

x=a; y=0; delta=0;           //начальная точка (x₀,y₀))

while (b2*x>a2*y)            //пока вектор касательной принадлежит третьей

      {                       //октанте

      point(x,y);             //ставим точку с координатами (x,y)

      if (delta<0)

            delta+=a2*(y*2+1);//положительное приращение

      else

            {                 //отрицательное приращение

            delta+=a2*(y*2+1)+b2*(-x*2+1);

            x—;              //x уменьшается на 1

            }

      y++;                    //y увеличивается на 1

      }

while (x>= 0)                //пока вектор касательной принадлежит

      {                       //четвертой октанте

      point(x, y);            //ставим точку с координатами (x,y)

      if (delta>=0)

            delta += b2*( -x*2 + 1 ); //отрицательное приращение

      else

            {                 //положительное приращение

            delta+=a2*(y*2+1)+b2*(-x*2+1);

            y++;

            }                 //y увеличивается на 1

      x—;                    //x уменьшается на 1

      }

getch();

closegraph();                //выход из графического режима

}

Результат работы программы