К методам одномерной оптимизации относятся методы дихотомического деления, золотого сечения, чисел Фибоначчи, полиномиальной аппроксимации и ряд их модификации.

Пусть задан отрезок [А, В], на котором имеется один минимум (в общем случае нечетное число минимумов). Согласно методу дихотомического деления (рис. 2.3, а) отрезок делят пополам и в точках, отстоящих от центра С отрезка на величину допустимой погрешности q, рассчитывают значения целевой функции F(C + q) и F(C - q). Если окажется, что F(C + q) > F(C — q), то минимум находится на отрезке [А,С], если F(C + q) < F(C — q), то минимум — на [С,В], если F(C + q) = F(C — q) — на [С — q, С + q]. Таким образом, на следующем шаге вместо отрезка [А, В] нужно исследовать суженный отрезок [A,С], [С, В] или [С — q,C + q]. Шаги повторяются, пока длина отрезка не уменьшится до значения погрешности q. Таким образом, требуется не более N шагов, где N – ближайшее к log ((B-A)/q) целое значение, но на каждом шаге целевую функцию следует вычислять дважды.

В соответствии с методом золотого сечения (рис. 2.3, б) внутри отрезка [А,В] выделяют две промежуточные точки С₁ и D₁ на расстоянии s = aL от его конечных точек, где L = В — А – длина отрезка. Затем вычисляют значения целевой функции F(x) в точках C₁ и D_1.  Если F(C₁) < F(D₁), то минимум находится на отрезке [A,D₁], если F(C₁) > F(D_l)), то — на отрезке [C₁ В], если F(C₁) = F(D_l) — на отрезке [С₁ D₁]. Следовательно, вместо отрезка [А,В] теперь можно рассматривать отрезок [A,D1], [С1 В] или [С1 , D1] т. е. длина отрезка уменьшилась не менее чем в L/(L — aL) = 1/(1 — а) раз. Если подобрать значение а так, что в полученном отрезке меньшей длины одна из промежуточных точек совпадет с промежуточной точкой от предыдущего шага, т. е. в случае выбора отрезка [А, D₁] точка D₂ совпадет с точкой С₁, а в случае выбора отрезка [С₁ В] точка С₂ – с точкой D₁, то это позволит сократить число вычислений целевой функции на всех шагах (кроме первого) в два раза.

Условие получения такого значения а формулируется следующим образом: (1 — 2a)L_k = aL_k-l, откуда с учетом того, что L_k /L_k_= 1/(1- а), имеем а = 0,382. Это значение и называют золотым сечением.

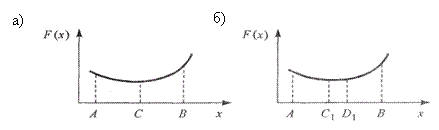
Рис. 2.3. Методы дихотомического деления (а) и золотого сечения (б)

Таким образом, требуется не более N шагов и N + 1 вычисление целевой функции, где N можно рассчитать, используя соотношение (В — А)1Е = (1 — d)N при заданной погрешности ε определения экстремума.

Согласно методу чисел Фибоначчи, используют числа Фибоначчи R, последовательность которых образуется по правилу R_i+2 = R_i+l + R_i  при R₀ = R₁ = 1, т. е. ряд чисел

Фибоначчи имеет вид 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 … Метод аналогичен методу золотого сечения с тем отличием, что коэффициент а равен отношению R_i-2/R_i, начальное значение z определяется из условия, что R должно быть наименьшим числом Фибоначчи, превышающим величину (В-А)/Е, где Е – заданная допустимая погрешность определения экстремума. Так, если (В — А)/Е = 100, то начальное значение i = 12, поскольку R₁= 144, и а = 55/144 = 0,3819, на следующем шаге будет а = 34/89 = 0,3820 и т. д.

В соответствии с методом полиномиальной аппроксимации при аппроксимации F(x) квадратичным полиномом

Р(х) = а₀ + a₁ x + a₂х²                                                               (2.7)

выбирают промежуточную точку С и в точках А, В, С вычисляют значения целевой функции. Далее решают систему из трех алгебраических уравнений, полученных подстановкой в (2.6) значений А, В, С  вместо х и вычисленных значений функции вместо Р(х). В результате становятся известными значения коэффициентов a_k в (2.6), и, исходя из условия ¶P(x)l¶x = 0, определяют экстремальную точку Э полинома. Например, если точка С выбрана в середине отрезка [А, В], то

Э = С + (С — A)(F(A) - F(B)) I (1(F(A) — 2F(C) + F(B))).