Среди методов нулевого порядка в САПР находят применение методы Розенброка, конфигураций, деформируемого многогранника, случайного поиска. К методам с использованием производных относятся методы наискорейшего спуска, сопряженных градиентов, переменной метрики.
Метод Розенброка является улучшенным вариантом метода покоординатного спуска.
Метод покоординатного спуска характеризуется выбором направлений поиска поочередно вдоль всех п координатных осей, шаг рассчитывается на основе одномерной оптимизации, критерий окончания поиска |Xk – Xk-n | < ε, где ε – заданная точность определения локального экстремума, п – размерность пространства управляемых параметров. Траектория покоординатного спуска для примера двумерного пространства управляемых параметров показана на рис. 2.4, где Xk – точки на траектории поиска, х – управляемые параметры. Целевая функция представлена своими линиями равного уровня, около каждой линии записано соответствующее ей значение F(X). Очевидно, что Э есть точка минимума.
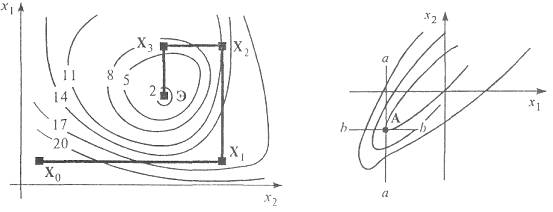
Рис. 2.4. Траектория покоординатного спуска
При использовании метода покоординатного спуска велика вероятность «застревания» поиска на дне оврага вдали от точки экстремума. На рис. 2.4 видно, что после попадания в точку А, расположенную на дне оврага, дальнейшие шаги возможны лишь в направлениях аа или bb, но они приводят к ухудшению целевой функции. Следовательно, поиск прекращается в точке А.
Примечание. Оврагом называют часть пространства управляемых параметров, в которой наблюдаются слабые изменения производных целевой функции по одним направлениям и значительные изменения с переменой знака по некоторым другим направлениям. Знак производной меняется в точках, принадлежащих дну оврага.
В то же время при благоприятной ориентации дна оврага, а именно при положении одной из координатных осей, близком к параллельности с дном оврага, поиск оказывается весьма быстрым. Эта ситуация показана на рис. 2.4.
Метод Розенброка заключается в таком повороте координатных осей, чтобы одна из них оказалась квазипараллельной дну оврага. Такой поворот осуществляют на основе данных, полученных после серии из п шагов покоординатного спуска. Положение новых осей si. может быть получено линейным преобразованием прежних осей хi: ось s1 совпадает по направлению с вектором Хk+n – Хk; остальные оси выбирают из условия ортогональности к X1 и друг к другу.
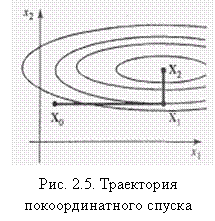Другой удачной модификацией покоординатного спуска является метод конфигураций (Хука — Дживса). В соответствии с этим методом вначале выполняют обычную серию из п шагов покоординатного спуска, затем делают дополнительный шаг в направлении вектора Xk – Xk-n, как показано на рис. 2.5, где дополнительный шаг выполняют в направлении вектора Х3 – X1, что и приводит в точку Х4.
Особенностью метода наискорейшего спуска является выполнение шагов поиска в градиентном направлении
Xk+1 = Xk + hk grad F(Xk) I |grad F(Xk)|,
шаг hk выбирается оптимальным с помощью одномерной оптимизации.
При использовании метода наискорейшего спуска, как и большинства других методов, эффективность поиска существенно снижается в овражных ситуациях. Траектория поиска приобретает зигзагообразный вид с медленным продвижением вдоль дна оврага в сторону экстремума. Чтобы повысить эффективность градиентных методов, используют несколько приемов.
Один из приемов, использованный в методе сопряженных градиентов (называемом также методом Флетчера – Ривса), основан на понятии сопряженности векторов. Векторы А и В называют Q-сопряженными, если ATQB = О, где Q – положительно определенная квадратная матрица того же порядка, что и размер N векторов А и В (частный случай сопряженности – ортогональность векторов, когда Q является единичной матрицей порядка N); Ат – вектор-строка; В – вектор-столбец.
Особенность сопряженных направлений для Q = Г, где Г – матрица Гессе, в задачах с квадратичной целевой функцией F(X) заключается в следующем: одномерная минимизация F(X) последовательно по N-сопряженным направлениям позволяет найти экстремальную точку не более, чем за N шагов.
Примечание. Матрицей Гессе называют матрицу вторых частных производных целевой функции по управляемым параметрам.
Основанием для использования поиска по N-сопряженным направлениям является то, что для функций F(X) общего вида может быть применена квадратичная аппроксимация, что на практике выливается в выполнение поиска более чем за N шагов.