Специфическая природа предикатов позволяет ввести над ними такие операции, которые не имеют аналогов среди операций над высказываниями. Имеются в виду две кванторные операции над предикатами.

Квантор общности

Для превращения одноместного предиката в высказывание нужно вместо его переменной подставить какой-нибудь конкретный предмет из области задания предиката. Имеется еще один способ для такого превращения – это применение к предикату операций связывания квантором общности или квантором существования. Каждая из этих операций ставит в соответствие одноместному предикату некоторое высказывание, истинное или ложное в зависимости от исходного предиката.

Определение. Операцией связывания квантором общности называется правило, по которому каждому одноместному предикату Р(х), определенному на множестве М, сопоставляется высказывание, обозначаемое , которое истинно в том и только в том случае, когда предикат Р(х) тождественно истинен, и  ложно в противном случае, то есть

Словесным аналогом квантору общности " является: «для любого», «для каждого», «для всякого» и т.п.

В выражении  переменная х уже перестает быть переменной в обычном смысле этого слова, то есть вместо нее невозможно подставить какие бы то ни было  конкретные значения. Говорят, что переменная х связанная.

Если одноместный предикат Р(х) задан на конечном множестве М = {a₁, a₂, …, a_n}, то высказывание  эквивалентно конъюнкции Р(а₁)  Р(а₂)   …  Р(а_n).

Пример 59.

Пусть х определен на множестве людей М, а Р(х) – предикат «х – смертен». Дать словесную формулировку предикатной формулы .

Решение.

Выражение  означает «все люди смертны». Оно не зависит от переменной х, а характеризует всех людей в целом, т. е. выражает суждение относительно всех х множества М.

Определение. Операцией связывания квантором общности по переменной х₁ называется правило, по которому каждому n-местному (n  2) предикату Р(х₁, х₂, …, х_n), определенному на множествах М₁, М₂, …, М_n, сопоставляется новый (n-1)-местный предикат, обозначаемый , который для любых предметов, превращается в высказывание , истинное в том и только в том случае, когда одноместный предикат , определенный на множестве М₁, тождественно истинен, и ложное в противном случае, то есть:

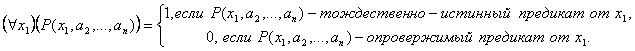
Квантор существования

Определение. Операцией связывания квантором существования  называется правило, по которому каждому одноместному предикату Р(х), определенному на множестве М, сопоставляется высказывание, обозначаемое , которое ложно в том и только в том случае, когда предикат Р(х) тождественно ложен, и  истинно в противном случае, то есть

Словесным аналогом квантору существования $ является: «существует», «найдется» и т.п.

Подобно выражению , в выражении  переменная х также перестает быть переменной в обычном смысле этого слова: это — связанная переменная.

Если одноместный предикат Р(х) задан на конечном множестве М = {a₁, a₂, …, a_n}, то высказывание  эквивалентно дизъюнкции Р(а₁)  Р(а₂)   …  Р(а_n).

Пример 60.

Пусть Р(х) – предикат «х – четное число», определенный на множестве N. Дать словесную формулировку высказыванию , определить его истинность.

Решение.

Исходный предикат Р(х): «х – четное число» является переменным высказыванием: при подстановке конкретного числа вместо переменной х он превращается в простое высказывание, являющееся истинным или ложным, например,

при подстановке числа 5 – ложным, при подстановке числа 10 – истинным. Высказывание  означает «во множестве натуральных чисел N существует четное число». Поскольку множество N содержит четные числа, то высказывание  истинно.

Определение. Операцией связывания квантором существования по переменной х₁ называется правило, по которому каждому n-местному (n  2) предикату Р(х₁, х₂, …, х_n), определенному на множествах М₁, М₂, …, М_n, сопоставляется новый (n-1)-местный предикат, обозначаемый , который для любых предметов, превращается в высказывание , ложное в том и только в том случае, когда одноместный предикат , определенный на множестве М₁, тождественно ложен, и истинное в противном случае, то есть:

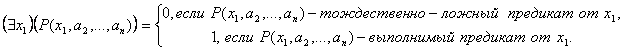
Выше уже было сказано, что переменная, на которую навешен квантор, называется связанной, несвязанная квантором переменная называется свободной. Выражение, на которое навешивается квантор, называется областью действия квантора и все вхождения переменной, на которую навешен квантор, в это выражение являются связанными. На многоместные предикаты можно на разные переменные навешивать различные кванторы, нельзя на одну и ту же переменную навешивать сразу два квантора.

Пример 61.

Пусть предикат Р(х, у) описывает отношение «х любит у» на множестве людей. Рассмотреть все варианты навешивания кванторов на обе переменные. Дать словесную интерпретацию полученных высказываний.

Решение.

Обозначим предикат «х любит у» через ЛЮБИТ(х, у). Предложения, соответствующие различным вариантам навешивания кванторов, проиллюстрированы на рис. 2.3-2.8, где х и у показаны на разных множествах, что является условностью и предпринято только для объяснения смысла предложений (реальные множества переменных х и у, очевидно, должны совпадать):

1)

 — «для любого человека х существует человек у, которого он любит» или «всякий человек кого-нибудь любит» (рис. 2.3).

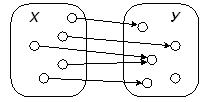
Рис. 2.3. Иллюстрация к высказыванию  «для любого человека х существует человек у, которого он любит» или «всякий человек кого-нибудь любит»

2)

 — «существует такой человек у, которого любит всякий человек х» (рис. 2.4).

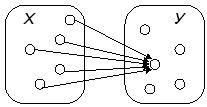
Рис. 2.4. Иллюстрация к высказыванию «существует такой человек у, которого любит всякий человек х»

3)

 — «все люди любят всех людей» (рис. 2.5).

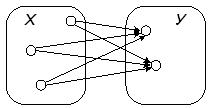
Рис. 2.5. Иллюстрация к высказыванию «все люди любят всех людей»

4)

 — «существует человек, который кого-то любит» (рис. 2.6).

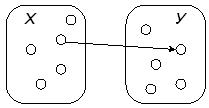
Рис. 2.6. Иллюстрация к высказыванию «существует человек, который кого-то любит»

5)

 — «существует человек, который любит всех людей» (рис. 2.7).

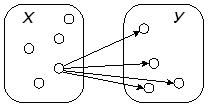
Рис. 2.7. Иллюстрация к высказыванию «существует человек, который любит всех людей»

6)

 — «для всякого человека существует человек, который его любит» или «каждого человека кто-то любит» (рис. 2.8).

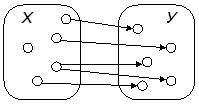
Рис. 2.8. Иллюстрация к высказыванию «для всякого человека существует человек, который его любит» или «каждого человека кто-то любит»

Из приведенного выше примера можно сделать вывод о том, что перестановка кванторов общности и существования меняет смысл высказывания, т.е. кванторы общности и существования не обладают в общем случае свойством коммутативности. Итак, одноименные кванторы можно менять местами, разноименные кванторы менять местами нельзя.