В задачах безусловной оптимизации необходимые условия представляют собой равенство нулю градиента целевой функции

grad F(X) = 0.

В общей задаче математического программирования (2.1) необходимые условия экстремума, называемые условиями Куна — Таккера, формулируются следующим образом.

Для того чтобы точка Э была экстремальной точкой выпуклой задачи математического программирования (ЗМП), необходимо наличие неотрицательных коэффициентов и_i,таких, что

и_i φ(Э) = 0, i= 1,2,3,…,m                                              (2.8)

и соблюдение при этом ограничений задачи, а также выполнение условия

grad F(Э)+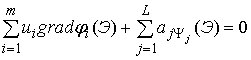,                     (2.9)

где т – число ограничений типа неравенств; L – то же типа равенств; а_j > 0 –коэффициенты.

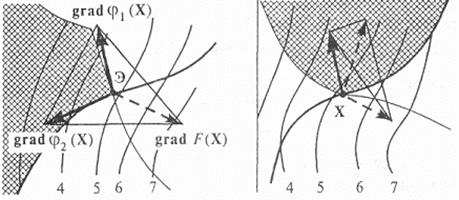
Рис. 2.6. Условия Куна – Таккера

За приведенной абстрактной формулировкой условий скрывается достаточно просто понимаемый геометрический смысл. Действительно, рассмотрим сначала случай с ограничениями только типа неравенств. Если максимум находится внутри допустимой области R, то, выбирая все и = О, добиваемся выполнения (2.8); если же точка максимума Э лежит на границе области R, то, как видно из левой части рис. 2.6, эту точку всегда соответствующим подбором неотрицательных и, можно поместить внутрь оболочки, натянутой на градиенты целевой функции F(X) и функций-ограничений φ_i(Х). Наоборот, если точка не является экстремальной, то (2.8) нельзя выполнить при любом выборе положительных коэффициентов и. (см. правую часть рис. 2.6, где рассматриваемая точка X лежит вне выпуклой оболочки, натянутой на градиенты). Учет ограничений типа равенств очевиден, если добавляется последняя из указанных в (2.9) сумма.