Пусть формулы А и В имеют одно и то же множество свободных переменных.

Определение. Формулы А и В равносильны в данной интерпретации, если на любом наборе значений свободных переменных они принимают одинаковые значения (т. е. если формулы выражают в данной интерпретации один и тот же предикат).

Определение. Формулы А и В равносильны на множестве М, если они равносильны во всех интерпретациях, заданных на множестве М.

Определение. Формулы А и В равносильны в логике предикатов, если они равносильны на всех множествах (АºВ).

Укажем несколько правил перехода от одних формул к другим, им равносильным.

Для формул логики предикатов сохраняются все равносильности и правила равносильных преобразований логики высказываний.

Утверждение. Всякую формулу логики предикатов, содержащую символы ® и », можно преобразовать в равносильную ей формулу, не содержащую этих символов.

Кроме этого, существуют следующие правила:

1) Перенос квантора через отрицание

2) Вынос квантора за скобки

3) Перестановка одноименных кванторов

"х "у А(х, у)  "у "х А(х, у),

$х $у А(х, у)  $у $х А(х, у).

4) Переименование связанных переменных.

Заменяя связанную переменную формулы А другой переменной, не входящей в эту формулу, в кванторе и всюду в области действия квантора получаем формулу, равносильную А.

Определение. Формула А, равносильная формуле В, и не содержащая символов ®, », а также составных формул под знаком отрицания, называется приведенной формой формулы В.

Теорема. Для любой формулы существует равносильная ей приведенная формула, причем множества свободных и связанных переменных этих формул совпадают.

Пример 66.

Преобразовать в приведенную форму формулу .

Решение.

Определение. Приведенная формула называется  нормальной (ПНФ), если она не содержит символов кванторов или все кванторы стоят в ее начале, а область действия каждого из них распространяется до конца формулы.

Пример 67.

Преобразовать в ПНФ формулы:

1) ;

2) .

Решение.

1)

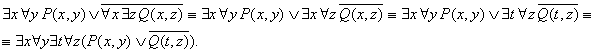
2)