На рис. 2.4 приведены законы распределения плотности тепловыделения, часто используемые при теплофизическом анализе технологических подсистем. Для простоты изображения эти законы даны для одномерных источников, поскольку из одномерных всегда можно сконструировать двух- или трехмерные законы.
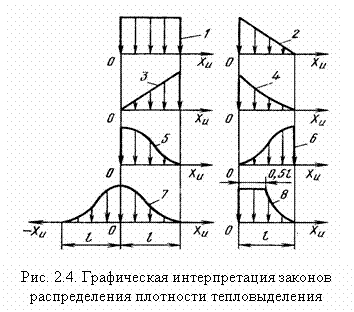
Математическое описание функций f(xn) приведено в табл. 2.3.
Таблица 2.3
Законы распределения
|
Код источника |
Закон |
Функция |
|
1 |
Равномерно распределенный |
|
|
2 |
Линейный |
|
|
3 |
|
|
|
4 |
Экспоненциальный |
|
|
5 |
Нормально распределённый несимметричный |
|
|
6 |
|
|
|
7 |
Нормально распределённый симметричный |
|
|
8 |
Комбинированный |
при |
;
; 
при 
;
Зная q0, можно рассчитать количество теплоты. На практике, как правило, решают обратную задачу. Известно количество теплоты Q или средняя мощность тепловыделения W за время τ требуется при заданном законе распределения определить наибольшую плотность q0. Полагая, что закон распределения не зависит от времени, и, подставляя выражение q(xи, yи, zи, τ)= q0f(xи, yи, zи, τ) в уравнение Q=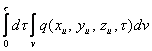
, получим
,
где 
.
Формула справедлива для одно-, двух- и трехмерных источников. Различие будет лишь в интеграле I, который для двумерного источника примет вид
,
а для одномерного
.