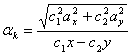Результат косвенного измерения (k) является функцией результатов прямых измерений х, у,…, z, т.е.

k = f (х, у,…, z).

Если результаты прямых измерений х, у,…, z распределены по нормальному закону, т.е. их доверительные интервалы

,

то в силу теоремы о дисперсии функции случайных величин

,

где

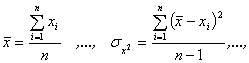
п – число повторных измерений (равное для всех прямых измерений).

Разделив обе части выражения для  на  и домножив их на t_a,, получим выражения для доверительного интервала погрешности результата косвенного измерения:

;

;

.

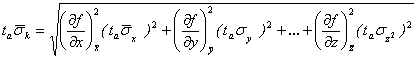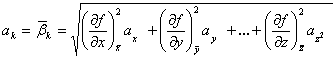Выражение для доверительного интервала в относительных единицах получим, разделив последнее выражение на k:

Если законы распределения результатов прямых измерений х, у,…, z неизвестны (т.е. их доверительные интервалы определены с учётом инструментальной погрешности а_х=Δ_х или ), то не удаётся достаточно строго получить формулу для доверительного интервала (а_k).

Часто при обработке результатов косвенных измерений исходят из положения, что при наименее благоприятном случае доверительный интервал результата косвенного измерения равен:

Такой способ определения а_k приводит к его завышенному значению, поскольку вероятность того, что истинные погрешности результатов прямых измерений одновременно будут иметь максимальные значения и одинаковый знак, практически равна нулю.

Более правильный результат даёт приближённая формула, основанная не на прямом, а на квадратичном суммировании:

;

.

Выражения для доверительных интервалов наиболее часто встречающихся функциональных зависимостей представлены в таблице 2.2.

Таблица 2.2