Напомним, что разбиением множества A называется семейство {Ai} его непустых попарно непересекающихся подмножеств, таких, что ÈiAi = A. Подмножества Ai называются блоками разбиения. Если в семействе учитывается порядок подмножеств, и если допускаются пустые блоки, то оно называется упорядоченным разбиением.
Упорядоченные разбиения и обобщенный бином Ньютона
Будем говорить, что упорядоченное разбиение ( A1, A2, …, Am ) множества E = {e1, e2, …, en} имеет тип ( k1, k2, …, km ), если |A1| = k1, |A2| = k2,…, |Am| = km. Число таких разбиений обозначается через
P(k1, k2, …, km)
или
Pn(k1, k2, …, km),
где n= k1 + k2 + … + km.
Лемма 1
.
Доказательство
Подмножество A1 можно выбрать 
способами. Подмножество A2 выбирается из оставшихся n-k1 элементов, его можно будет выбрать 
способами. Подмножество A3 можно будет выбрать 
способами, и т.д. Выбор подмножества Am определен предшествующими подмножествами. Отсюда получаем:
.
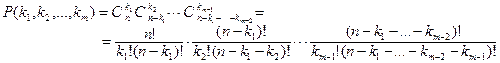Поскольку n – k1 – … – km-1 = km, то после сокращения дроби получаем нужное равенство.
Теорема 1
.
Доказательство
Рассмотрим как ящики сомножители произведения:
.
Произведение состоит из слагаемых вида 
. Каждое такое слагаемое встречается столько раз, сколько существует упорядоченных разбиений множества ящиков. Разбиение будет состоять из следующих подмножеств: первое подмножество состоит из ящиков, откуда выбран x1, второе состоит из подмножеств, откуда выбран x2 и т.д. Отсюда коэффициент при будет равен P(k1, k2, …, km). Что и требовалось доказать.
Разбиения и перечисление сюръекций
Пусть {B1, …, Bk} – разбиение множества X, состоящего из n элементов. Обозначим через Pk(X) множество разбиений X на k блоков, а через P(X) – множество всех
разбиений. Число S(n,k) = |Pk(X)| называется числом Стирлинга второго рода, Bn=|P(X)| – числом Белла. Ясно, что 
.
Каждому разбиению мы сопоставили отношение эквивалентности и заметили, что разбиения составляют решетку относительно включения соответствующих отношений эквивалентности. Отсюда множество разбиений будет решеткой относительно неравенства p£s Û, каждый блок B Î s является объединением некоторых блоков из p.
Например, {{1},{2},{3}}£{{1},{2,3}}. Пусть sn,k – число сюръекций f:{1,2, ×××,n}® {1,2, …, k}. Каждой сюръекции соответствует разбиение {f –1(y): 1 £ y £ k}. Отсюда легко видеть, что sn,k =k!S(n,k). Положим S(0,0)=1.
Пример 2
Число S(4,2) равно 7, ибо все разбиения множества {1,2,3,4, 5, 6, 7} на два блока исчерпываются следующими множествами:
{{1},{2,3,4}}, {{2},{1,3,4}}, {{3},{1,2,4}}, {{4},{1,2,3}},
{{1,2},{3,4}}, {{1,3},{2,4}}, {{1,4},{2,3}}.
Теорема 2
Имеют место следующие свойства чисел Стирлинга второго рода:
1) S(n,k)=0, при k > n;
2) S(n,0) = 0 и S(n,n) = 1, при n > 0;
3) S(n,k) = S(n-1,k – 1) + kS(n – 1, k), при 0 < k < n.
Доказательство
Докажем последнее соотношение. Множество разбиений множества {1,2, ×××,n} состоит из двух классов:
1) разбиения, содержащие блок {n};
2) разбиения, для которых n принадлежит блокам, имеющим более одного элемента.
В первом классе S(n – 1, k – 1) разбиений. Во втором классе получаем kS(n – 1, k) разбиений, ибо каждому разбиению множества {1, 2, ×××, n – 1} на k блоков B1, B2, ×××, Bk соответствует k разбиений
B1 È {n}, B2, …, Bk;
B1, B2È {n}, …, Bk;
×××××××××××××××××××××××××××××××
B1, B2, …, Bk È {n},
Следовательно, S(n,k) = S(n – 1, k – 1) + kS(n – 1,k), при 0 < k < n. Составим таблицу 2.3 для нахождения чисел Стирлинга.
Таблица 2.3 Числа Стирлинга
|
n k |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
1 |
||||||||
|
2 |
1 |
1 |
|||||||
|
3 |
1 |
3 |
1 |
||||||
|
4 |
1 |
7 |
6 |
1 |
|||||
|
5 |
1 |
15 |
25 |
10 |
1 |
||||
|
6 |
1 |
31 |
90 |
65 |
15 |
1 |
|||
|
7 |
1 |
63 |
301 |
350 |
140 |
21 |
1 |
||
|
8 |
1 |
127 |
966 |
1701 |
1050 |
266 |
28 |
1 |
|
|
9 |
1 |
255 |
3025 |
7770 |
6951 |
2646 |
462 |
36 |
1 |
|
10 |
1 |
511 |
9330 |
34105 |
42525 |
22827 |
5880 |
750 |
45 |
Пример 3
Найдем число сюръекций {1,2,3,4,5,6}®{1,2,3,4}. Оно равно 4!S(6,4). Число S(6,4) находим из таблицы 2.3. Отсюда искомое число равно:
4!∙65 = 1∙2∙3∙4∙65 = 1560.
Положим B0 = 1. Число Белла Bn можно вычислить по формуле:
.
Рассмотрим более простые формулы для нахождения чисел Белла.
Теорема 3
, "n ³ 0.
Доказательство
Множество разбиений X = {1,2, …, n+1} состоит из классов, зависящих от блока A, содержащего n + 1. Для таких A будет справедливо включение:
XA Í{1, 2, …, n}.
Отсюда каждое разбиение можно получить, выбрав блок A ‘ (n + 1) и разбиение pÎP(XA). Выбор блока A с количеством элементов |A| = k + 1 будет осуществляться выбором подмножества из {1,2, …, n}, состоящего из k элементов.
Следовательно:
.
Упражнения
Размещения
Рис. 2.4. Пример флага
1. Сколькими способами можно составить трехцветный флаг (рис. 2.4) из материалов семи цветов. Одна из полос должна быть красной.
Ответ: 73 — 63.
2. Сколькими способами можно раскрасить 4 полосы флага в 7 цветов, так, чтобы, по крайней мере, две полосы имели одинаковый цвет?
Ответ: 
.
3. Сколькими способами можно раскрасить 4 полосы флага в 7 цветов, так, чтобы рядом находящиеся полосы имели различные цвета?
Ответ: 7∙ 63.
4. Сколько перестановок p {1,2, …, 5} ® {1,2, …, 5} удовлетворяют условию p(1)¹ 2?
5. В соревновании принимают участие 8 спортсменов. Сколькими способами могут быть разделены медали (золотые, серебряные и бронзовые)?
6. Найти число функций {1,2,3}®{1,2,3,4,5}.
7. Найти число инъекций {1,2,3}®{1,2,3,4,5}.
8. Сколько чисел между 1000 и 10000 состоят из различных цифр?
9. Сколько семизначных чисел (не начинающихся с 0) состоят из различных цифр?
Сочетания
10. Доказать тождества непосредственно из определения числа 
:
1) 
;
2) 
;
3) 
.
11. Из содержащей 52 карты колоды вынимают 10 карт. Какова вероятность, что среди них окажется
1) хотя бы один туз? Ответ: 
2) ровно один туз? Ответ: 
3) не менее двух тузов? Ответ: 
4) ровно два туза? Ответ: 
12. Из содержащей 52 карты колоды вынимают 10 карт. Какова вероятность, что среди них окажется
1) 4 туза, 2 короля, 3 дамы;
2) 2 туза, 2 короля, 2 дамы;
3) 1 туз, 1 короля, 2 дамы, 3 десятки;
4) 4 туза, 4 короля, 2 дамы;
5) 2 туза, 3 короля, 1 дама, 1 десятка;
6) 3 туза, 2 короля, 4 дамы.
13. Разложением числа m называется конечная последовательность (x1, x2, ×××, xn) неотрицательных целых чисел, таких, что x1+ x2+ ××× + xn = m. Сколько разложений числа 19 состоит лишь из чисел 2 и 3?
Указание. Если в разложении p двоек и q троек, то 2p + 3q = 19. Отсюда получаем следующие варианты разложения:
|
p = 2 |
q = 5 |
число разложений |
|
p = 5 |
q = 3 |
число разложений |
|
p = 8 |
Q = 1 |
число разложений |
Ответ: 
.
1. Сколько разложений числа 12 состоит из чисел 2 и 3?
Ответ: 
= 12.
2. Сколькими способами можно разложить число 1024 в произведение трех натуральных чисел, каждое из которых больше 1?
Указание. Это число решений уравнения x1+ x2,+ x3 = 10, где xi > 0.
Ответ: 
= 36.
3. Сколько существует на плоскости непрерывных путей из точки (0,0) в точку (n,n) Î N ´ N, состоящих из направленных отрезков, вектора которых равны (1,0) или (0,1)?
4. Найти число непрерывных путей в декартовой плоскости, соединяющих точку (0,0) с точкой (m,n) Î N´N, проходящих через точку (p,q) и состоящих из направленных отрезков, вектора которых равны (1,0) или (0,1)?
5. Найти число решений уравнения x1+ x2+ x3+ x4 + x5 = 20, где xi > 0.
6. Найти число решений уравнения x1+ x2+ x3+ x4 + x5 = 15, где xi ³ 0.
7. Найти число возрастающих функций {1,2,3,4,5}®{1,2,3,4,5,6,7}.
8. Найти число неубывающих сюръекций {1,2,3,4,5,6,7}®{1,2,3,4,5}.
9. Найти число неубывающих функций {1,2,3,4,5}®{1,2,3,4,5}.
10. Найти количество десятичных неотрицательных целых чисел, состоящих из не более, чем n цифр, расположенных в неубывающем порядке (цифра 0 не допускается первой для ненулевых чисел). Например, при n = 2, такие числа будут равны:
0
1, 2, 3, 4, 5, 6, 7, 8, 9,
11, 12, 13, 14, 15, 16, 17, 18, 19, 22, 23, …∙, 89, 99.
Ответ: 
= 36.
11. Найти количество десятичных неотрицательных целых чисел, состоящих цифр, расположенных в возрастающем порядке.
Ответ: 
12. Найти число неотрицательных целых чисел, десятичная запись которых состоит из n разрядов и содержит все цифры, расположенные в невозрастающем порядке.
Ответ: 
.
13. Какое количество m ´ n-матриц можно составить из неотрицательных целых чисел aij ³ 0, таких, что S aij = k.
Ответ: 
.
Упорядоченные разбиения
14. Десять человек разбились на 5 групп по 2 человека в каждой. Скольким способами это можно сделать?
Указание. Количество упорядоченных разбиений равно 10!/(2!2!2!2!2!). При перестановках групп получаются одинаковые разбиения, отсюда искомое число равно:
10!/(2!2!2!2!2!)/5! = 1×3×5×7×9 = 945.
1. В группе 20 студентов. Одному человеку положено выдать надбавку к стипендии в размере 1000 рублей, двум – по 500, трем – по 300. Сколькими способами это можно сделать?
2. Сколько существует шашечных позиций, состоящих из 10 белых и 10 черных шашек?
3. Сколько различных слов можно составить с помощью перестановок всех букв слова МАТЕМАТИКА. Словом называется произвольная конечная последовательность букв.
4. Оценить число шахматных позиций, содержащих все фигуры и пешки?
5. В урне находится k шаров. Каждый шар может иметь либо белый, либо черный, либо красный цвет. Какова вероятность того, что один шар белый, один – черный (а остальные красные)?
Ответ: k(k – 1)/3k.
6. Найти коэффициент при 
в разложении степени 
в сумму однородных одночленов.
7. Найти (x1 + x2 + x3)4.
8. Сколько путей, составленных из направленных отрезков единичной длины, существует в трехмерной решетке из (0,0,0) в (p,q,r). Вектора отрезков равны (1,0,0), (0,1,0), (0,0,1).
Формула включения и исключения
9. Сколько чисел из принадлежащих множеству {1, 2, …, 1000} не делится ни на 10, ни на 12, ни на 9?
10. Группа из 20 студентов сдает зачеты по математике, физике и информатике. Множество студентов, сдавших математику и физику совпадает с множеством студентов, сдавших математику и информатику, и совпадает с множеством студентов, сдавших физику и информатику. Каждый студент сдал, по крайней мере, один зачет. Найти число студентов, сдавших все зачеты, если математику сдали 15, физику – 16, информатику – 17 студентов.
Неупорядоченные разбиения
11. Найти число разбиений множества {1,2,3,4,5,6,7} на 3 блока.
12. Найти число разбиений множества, состоящего из 8 элементов.
13. Найти число сюръекций {1,2,3,4,5,6,7}®{1,2,3,4}.
14. Вывести формулу для числа сюръекций {1, 2, …, m}®{1, 2, …, n} с помощью формулы включения и исключения для подсчета числа несюръективных отображений |U1È×××È Un|, где Ui – множество отображений, образ которых не содержит элемент i.