Словесная запись алгоритма
Словесная форма записи обычно используется для алгоритмов, ориентированных на исполнителя – человека. Команды алгоритмов нумеруют, чтобы иметь возможность на них ссылаться.
Пример 1
Вася действует по следующему алгоритму:
· шаг 1. Пройти 4 м прямо;
· шаг 2. Повернуть направо и пройти еще 3 м;
· шаг 3. Повторять шаг 2, пока не будет пройдено всего 25 м;
· шаг 4. Остановиться.
Определить расстояние от точки начала до точки финиша.
Решение
Представим решение в графическом виде (рис. 2.1):
1) Вася доходит до точки Д в первый раз, пройдя:
4 + 3 + 3 + 3 = 13 метров;
2) далее он поочередно попадает в точки:
· А (16 метров);
· В (19 метров);
· С (22 метра);
· Д (25 метров). Задача выполнена, Вася прошел 25 метров;
3) Расстояние от точки старта до точки финиша (Д) равно 1 метр.
Рассмотрим словесную запись алгоритма Евклида.
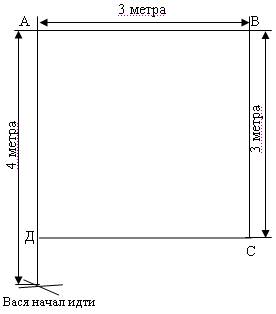
Рис. 2.1. Определение расстояния от точки начала до точки финиша
Пример 2
Значениями переменных а и b являются натуральные числа. Пусть a = 60 и b = 36 тогда в результате работы следующего алгоритма:
1) если a = b, то работа алгоритма закончена; иначе выполняется пункт 2;
1) если a > b, то переменной a присваивается значение a – b; иначе переменной b присваивается значение b – a;
2) выполняется условие 1 данного алгоритма.
Определить значение переменной а.
Решение
Шаг 1
1) проверим первое условие алгоритма a = b. Так как a = 60 и b = 36, то 
, следовательно, переходим к пункту 2;
2) проверим условие 2. Так как условие а > b, 60 > 36 выполняется, следовательно а = а – b, т.е. а = 60 – 36 = 24. Переходим к пункту 3;
3) переходим к пункту 1;
Шаг 2
1) проверим условие алгоритма a = b. Так как a = 24 и b = 36, то 
, следовательно, переходим к пункту 2;
2) проверим условие 2. Условие а > b (24 > 36) не выполняется, следовательно b > a (36 > 24) выполняется, получаем b = b – a = 36 – 24 = 12, переходим к пункту 3;
3) переходим к пункту 1;
Шаг 3
1) проверим условие алгоритма a = b. Так как a = 24 и b = 12, то 
, следовательно, переходим к пункту 2;
2) проверим условие 2. Так как условие а > b (24 > 12) выполняется, следовательно, a = a – b = 24 – 12 = 12, переходим к пункту 3;
3) переходим к пункту 1;
Шаг 4
1) проверим условие алгоритма a = b. Так как а = 12 и b = 12, то 12 = 12. Условие 1 выполняется, работа алгоритма закончена.
Ответ: а = 12.
Схематичная запись алгоритма
Схемы (блок-схемы) представляют алгоритм в наглядной графической форме. Команды алгоритма помещаются внутрь блоков, соединенных стрелками, показывающими очередность выполнения команд алгоритма. Приняты определенные стандарты изображений блоков. Основные блоки, используемые для записи алгоритмов, представлены на рис. 2.2.
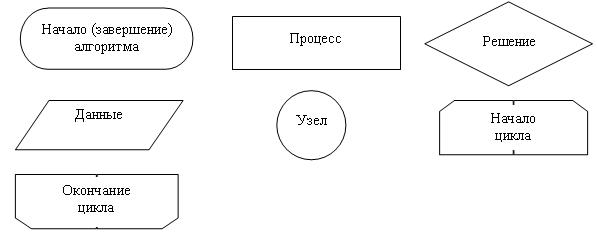
Рис. 2.1. Основные блоки, используемые для записи алгоритмов
Для записи блоков команды используется естественный язык с элементами математической символики. В результате проверки условия возникают два возможных
пути для продолжения алгоритма. Эти пути изображаются стрелками со знаками «+» и «-» (иногда используют «Да» или «Нет»). Переход по стрелке со знаком «+» происходит, если условие соблюдено, а переход по стрелке «-», если условие не соблюдено.
Запишем решение задачи заданной с помощью блок-схемы (рис. 2.3):
1) начинаем алгоритм;
2) присваиваем переменным значения:
Х = 3, У = 5;
3) переходим к выполнению условия (ромб), если Х < Y, то идем в сторону «Да». Проверяем: 3 < 5. Идем в сторону «Да»;
4) находим значение переменной:
S = X + Y = 3 + 5 = 8;
5) подходим к окончанию алгоритма (конец).
Ответ: S = 8.
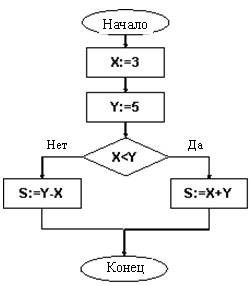
Рис. 2.3. Блок-схема задачи