Эксперимент, в процессе которого исследуется функциональная зависимость одной величины от другой (у = f(х)), называется однофакторным экспериментом.

Независимая переменная (х) называется фактором, зависимая переменная (у) называется функцией отклика.

Эксперимент состоит из совокупности опытов. Под опытом будем понимать прямое или косвенное измерение функции отклика (у) при данном значении фактора (х). Опыт может состоять как из однократного измерения (прямого или косвенного), так и из п повторных измерений.

Для предварительного анализа результатов однофакторного эксперимента их представляют в виде графиков с помощью быстрых и простых методов, например метода контура. Метод контура состоит в том, что построенное поле точек (результатов опытов) обводят контуром. По оси поля, очерченного этим контуром, проводят «на глаз» искомую кривую.

Часто перед исследователем стоит задача: представить результаты однофакторного эксперимента в виде эмпирической функциональной зависимости у = f(х). Такая зависимость называется уравнением регрессии. Подбор вида уравнения регрессии (параболическое, гиперболическое, показательное, логарифмическое) проводят с помощью функциональных шкал.

Функциональной шкалой называется шкала, масштаб которой непостоянен, а изменяется по определённому закону. Если опытные точки, нанесённые на график с функциональной шкалой, ложатся вдоль прямой, то для построения уравнения регрессии следует использовать закон изменения масштаба этой функциональной шкалы.

Постоянные коэффициенты в уравнении регрессии определяются с помощью метода наименьших квадратов (МНК). В теории вероятностей доказывается теорема о МНК, согласно которой наиболее вероятными значениями постоянных коэффициентов будут те, при которых сумма квадратов отклонений экспериментальных значений функции отклика от её расчётных значений будет минимальной.

Пусть у_j – экспериментальные значения функции отклика, f(x_j) – её расчётные значения,  ε = у_j – f(x_j) – отклонения экспериментальных и расчётных значений, т – число постоянных коэффициентов в уравнении регрессии. В силу указанной теоремы для определения коэффициентов необходимо найти частные производные от функции (N – число опытов) по каждому из коэффициентов и приравнять их нулю. Проделав эту операцию, мы получим систему из т уравнений с т неизвестными. Решив указанную систему, получим выражения для коэффициентов уравнения регрессии.

В качестве примера рассмотрим выражения для коэффициентов линейного уравнения регрессии:

у = b₀ + b₁x.

Обозначим функцию через S:

,

тогда

;

.

Приравняв и нулю, получаем систему из двух уравнений;

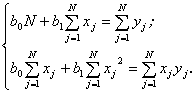
Решив систему относительно b₀ и b₁, получим искомые выражения:

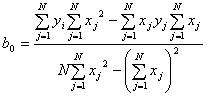;                                       (2.1)

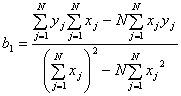.                                          (2.2)

Расчёт коэффициентов вручную весьма трудоёмок. Обычно их рассчитывают с помощью стандартных программ на ЭВМ. Однако стандартные программы приспособлены только для расчёта коэффициентов линейных уравнений регрессии. Поэтому перед расчётом коэффициентов на ЭВМ уравнение регрессии у = f (х) приводят к линейному виду заменой переменных.