Начальные условия отвечают на вопрос о том, каково было температурное поле в момент вре­мени, принятый за начало отсчета. Они описываются выраже­нием . Очень часто температура компонентов технологических подсистем в начальный момент времени может быть принята равной температуре  окружающей среды, т. е. . В этом случае удобно, как отмечалось выше, вести расчет в так называемых избыточных температурах, условно считая, что , а затем по окончании расчета к ре­зультату прибавляя  . Граничными называются условия взаимодействия поверх­ностей тел с окружающей средой или другими телами. Различают несколько разновидностей граничных условий. При граничных условиях первого рода (ГУ1) предполагают, что известен закон распределения температур на граничных поверхностях тела . Пусть, например, требуется определить темпе­ратурное поле внутри какой-либо детали или инструмента. Сде­лать это экспериментальным путем, не разрушая объект измерения, довольно трудно, измерить же температуру на поверхности де­тали, инструмента или другого твердого тела экспериментальным путем значительно проще, это может быть выполнено без повреж­дения объекта. Если мы знаем ГУ1 в виде закона распределения температур на поверхностях тела, то, решая дифференциальное уравнение теплопроводности, можем рассчитать поле температур внутри детали, инструмента и т. д. Частным случаем ГУ1 яв­ляется условие изотермичности поверхностей тела, т. е. .

Граничные условия второго рода (ГУ2) предусматривают, что известен закон распределения плотности тепловых потоков , следующих через граничные поверхности. В частном случае . Это означает, что рассматриваемая поверхность не обменивается теплотой с окружающей средой, т. е. является адиабатической. Выполняя тепловые расчеты, относящиеся к технологическим подсистемам, во многих случаях с достаточной для практики точностью можно пренебречь теплообменом той или иной поверхности (или ее участка) с окружающей средой, т. е. принять , что упрощает расчет.

Граничные условия третьего рода (ГУЗ) используют в том случае, когда теплообменом поверхности с окружающей средой пренебречь нельзя. В этом случае должны быть заданы температура  среды, с которой соприкасается данное тело, и так называемый коэффициент теплоотдачи , Вт/(м² × °С), характеризующий теплообмен между средой и поверхностью.

Согласно закону Ньютона-Рихмана плотность теплового потока пропорциональна разности температур поверхности  и окружающей ее среды , т. е.

.                                                         (2.1)

Формула (2.1) дает возможность определить количество теп­лоты , Вт/м², которое в единицу времени с единицы поверхности отводится в окружающую среду. Как следует из закона Фурье, к поверхности тела подводится поток

.

Следовательно,

 или .                                (2.2)

Выражение (2.2) представляет собой математическое описание граничных условий третьего рода.

Граничные условия четвертого рода (ГУ4) возникают тогда, когда рассматриваемое твердое тело находится в беззазорном контакте с другим твердым телом и между ними происходит теплообмен. Этот вариант граничных условий весьма часто встре­чается в теплофизике технологических процессов. Например, при обработке давлением детали штампа практически беззазорно соприкасаются с обрабатываемой заготовкой; при резании ме­талла поверхности инструмента на определенных участках сопри­касаются со стружкой и заготовкой. При граничных условиях четвертого рода, когда контакт между телами идеален, темпе­ратура в любой точке поверхности соприкосновения как со сто­роны одного, так и со стороны другого тела одна и та же, т. е.

                                                            (2.3)

С целью упрощения расчетов часто вместо равенства темпе­ратур в каждой точке контакта в качестве ГУ4 принимают равенство средних температур на поверхности контакта, т. е. вместо формулы (2.3) полагают

.

Граничные условия четвертого рода используют при решении балансовых задач, т. е. при анализе распределения теплоты между телами, находящимися в контакте. Распределив между соприкасающимися телами теплоту, образующуюся на контактной поверхности, и рассчитав плотность теплового потока в каждом из тел, далее пользуются граничными условиями второго рода.

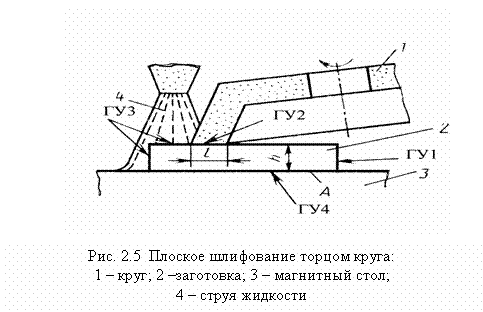
Заканчивая рассмотрение вопроса о граничных условиях, отметим, что на разных участках реальных тел могут иметь место различные граничные условия. Рассмотрим, например, процесс плоского шлифования заготовки торцом чашечного круга (см. рис. 2.5). Если решена задача о распределении теплоты шлифо­вания между кругом и заготовкой, то по отношению к заготовке имеем следующие граничные условия: ГУ3 — на поверхности соприкосновения с жидкостью; ГУ2 — на контактной поверхности с кругом, где известна плотность теплового потока, и на торце заготовки, который можно считать адиабатическим, если пре­небречь его теплоотдачей в воздух; ГУ4 — на поверхности, где заготовка соприкасается с магнитным столом станка.