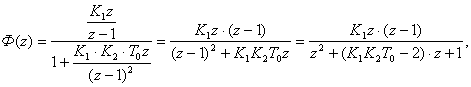Рассмотрим несколько дискретных систем, структурные схемы которых отличаются друг от друга расположением квантователя. Это различие определяет не только вид передаточной функции, но и возможность ее определения.
1) Система с квантованием сигнала ошибки (рис. 2.5).
Система описывается следующим уравнением в Z-изображениях:
(2.10)
Откуда 
.
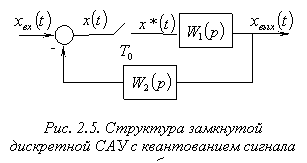Далее необходимо выполнить Z-преобразование над обеими частями последнего равенства. При этом следует учитывать, что такое преобразование от произведения импульсной функции (помеченной символом *) и непрерывной функции равно произведению Z-изображений, соответствующих этим функциям.
Следовательно,
;
.
Выполнив Z-преобразование второго уравнения системы (2.10), получим:
.
Z-изображение выходного сигнала:
а передаточная функция замкнутой системы:
(2.11)
1) 
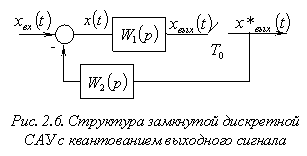Система с импульсным элементом на выходе (рис. 2.6).
Дискретная система с импульсным элементом на выходе описывается следующими уравнениями:
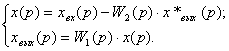
Подставляя первое из приведенных уравнений во второе, получим:
Z-преобразование последнего выражения дает:
откуда
.
В отличие от системы (рис. 2.5) в данной системе (рис. 2.6) невозможно определить передаточную функцию в виде:
.
2) Система с квантованием выходного сигнала и сигнала ошибки (рис. 2.7).
Преобразование Лапласа для сигнала ошибки и выходного сигнала имеет вид:
.
Z-преобразование над приведенными уравнениями дает:
и 
.
Z-изображение выходного сигнала:
Следовательно:
а передаточная функция замкнутой системы:
.
Пример 13
Для системы, структура которой приведена на рис. 2.8, необходимо определить передаточную функцию замкнутой САУ и передаточную функцию по ошибке.
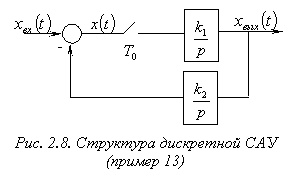Для замкнутой дискретной САУ с квантованием сигнала ошибки дискретная передаточная функция 
и передаточная функция по ошибке могут быть найдены по следующим формулам:
(2.12)
(2.13)
где 
– дискретные передаточные функции прямого канала и разомкнутой системы, соответственно.
Для системы (рис. 2.8):
,
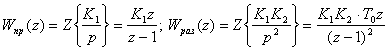Следовательно,
