Пусть имеем задачу линейного программирования, заданную в общей форме записи:

                        (2.20)

Двойственная задача по отношению к задаче (2.20) запишется следующим образом:

                       (2.21)

Для построения двойственной задачи необходимо соблюдать следующие правила:

1) каждому -му ограничению задачи (2.20) соответствует переменная  задачи (2.21), и наоборот, каждому -му ограничению двойственной задачи (2.21) соответствует переменная  задачи (2.20);

2) матрица системы ограничений двойственной задачи получается из матрицы системы ограничений исходной задачи транспонированием, т.е. заменой строк столбцами, с сохранением порядка;

3) свободные члены ограничений задачи (2.20) являются коэффициентами при соответствующих переменных целевой функции двойственной задачи (2.21); аналогично коэффициенты целевой функции исходной задачи (2.20) совпадают со свободными членами системы ограничений двойственной задачи (2.21);

4) если целевая функция исходной задачи (2.20) максимизируется, то целевая функция двойственной задачи (2.21) минимизируется;

5) в задаче (2.20) ограничения неравенства следует записывать со знаком , а для здачи (2.21) – со знаком ;

6) если на -ю переменную задачи (2.20) наложено условие неотрицательности, то -е ограничение задачи (2.21) будет неравенством, в противном случае -е ограничение будет равенством; аналогично связаны между собой ограничения задачи (2.20) и переменные задачи (2.21).

Пример

Построить двойственную задачу к задаче:

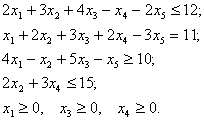
Решение

Упорядочим исходную задачу. Так как требуется найти максимум целевой функции, то ограничения-неравенства должны быть записаны со знаком . Умножим третье неравенство на (-1), приведем систему ограничений к виду (2.20):

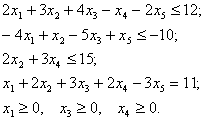
Двойственная задача будет иметь четыре переменные , так как исходная задача содержит четыре ограничения. В соответствии с указанными правилами запишем двойственную задачу:

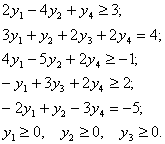
Второе и пятое ограничения двойственной задачи записаны в виде равенств, так как на соответствующие им переменные  и  в исходной задаче не наложено условие неотрицательности. На переменные  наложено условие неотрицательности в связи с тем, что в исходной задаче, приведенной к виду (2.20), им соответствуют ограничения-неравенства.