Всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в контуре. Электрическое поле, возбуждаемое магнитным полем, как и само магнитное поле, является вихревым (силовые линии замкнуты).
В свою очередь, всякое изменение электрического поля должно вызывать появление в окружающем пространстве вихревого магнитного поля. Для установления количественных соотношений между изменяющимся электрическим полем и вызываемым им магнитным полем Максвелл ввел так называемый ток смещения.
![]() ,
,
где ![]() – плотность тока смещения; dS – площадь сечения, по которому течет ток смещения.
– плотность тока смещения; dS – площадь сечения, по которому течет ток смещения.
В диэлектриках ток смещения состоит из двух слагаемых:
![]() ,
,
где ![]() – плотность тока смещения в вакууме;
– плотность тока смещения в вакууме; ![]() – плотность тока поляризации – тока, обусловленного упорядоченным движением электрических зарядов в диэлектрике (смещения зарядов в неполярных молекулах или поворота диполей в полярных молекулах).
– плотность тока поляризации – тока, обусловленного упорядоченным движением электрических зарядов в диэлектрике (смещения зарядов в неполярных молекулах или поворота диполей в полярных молекулах).
Полная система уравнений Максвелла в интегральной форме:
1) ![]() ; 2)
; 2) 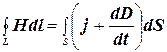 ;
;
3) ![]() ; 4)
; 4) ![]() ;
;
где r – объемная плотность заряда.
Полная система уравнений Максвелла в дифференциальной форме:
1) ![]() ; 2)
; 2) ![]() ;
;
3) ![]() ; 4)
; 4) ![]() ;
;
где j – плотность тока проводимости; первое уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля; второе уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями; третье уравнение показывает, что электростатичекое поле обусловлено электрическими зарядами; четвёртое уравнение показывает, что внутри замкнутой поверхности магнитное поле равно нулю.