2.6. Теоремы двойственности | Электронная библиотека

Гуманитарные науки / Теория системного анализа и принятия решений / 2.6. Теоремы двойственности

Для пары взаимодвойственных задач (2.20) и (2.21) имеют место следующие теоремы двойственности.

Теорема 1

Если одна из задач двойственной пары имеет решение, то другая задача также имеет решение. При этом для любых оптимальных планов

имеет место равенство

Следствие 1. Для разрешимости одной из задач двойственной пары необходимо и достаточно, чтобы каждая из задач имела хотя бы одно решение.

Следствие 2. Если целевая функция одной из задач двойственной пары не ограничена, то другая задача не имеет решения.

Следствие 3. Для оптимальности планов

пары двойственных задач необходимо и достаточно выполнение равенства

Теорема 2

Для оптимальности допустимых планов и пары двойственных задач (2.20) и (2.21) соответственно необходимо и достаточно, чтобы они удовлетворяли системе уравнений:

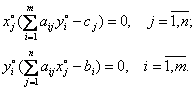
Теорема справедлива для симметричной двойственной пары задач. Она позволяет определить оптимальное решение одной из пары задач по решению другой. Это можно сделать, например, с помощью таблицы взаимодвойственных задач (табл.2.13). В таблице2.13 значения базисных переменных исходной задачи определяются соответственно элементами -го столбца двойственной задачи, а значения базисных переменных двойственной задачи – элементами -й строки исходной задачи.

Таблица 2.13 Таблица взаимодвойственных задач

	БП
СП	СП БП	СЭ

…	…	…	………

1		0

Пример 1

Найти решение исходной задачи путем графического анализа двойственной к ней:

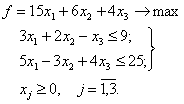
Решение

Двойственная задача имеет вид:

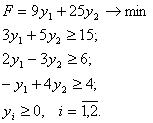
Графическое решение двойственной задачи дает следующий результат:

Подставляя полученное решение в систему ограничений двойственной задачи, находим:

;

Первое ограничение удовлетворяется как строгое неравенство, следовательно, по теореме 2 переменная . Так как и , то согласно теореме 2 оба ограничения в исходной задаче удовлетворяются как равенства.

Подставляя в исходную систему, находим:

откуда

Тогда оптимальное решение:

для которого по теореме 1 значение целевой функции

Пример 2

Построить двойственную задачу, решить одну из них и записать решение другой задачи, если исходная задача имеет вид

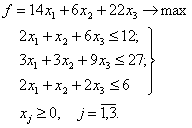
Решение

Двойственная задача запишется в виде:

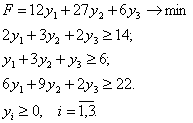
Установим соответствие между переменными пары двойственных задач. Приводя задачи к канонической форме, будем иметь системы ограничений исходной и двойственной задач, содержащие одинаковое число переменных. В нашем случае таких переменных будет шесть. Базисные переменные исходной задачи соответствуют свободным переменным двойственной задачи. Аналогично свободные переменные двойственной задачи соответствуют свободным переменным исходной задачи. Решим исходную задачу симплексным методом. Занесем данные обеих задач в табл. 2.13 получим табл. 2.14.