Напомним, что для того, чтобы функция, определенная обычным образом, получила доступ ко всем членам класса, включая закрытые, ее следует объявить дружественной, указав в теле класса ее прототип с ключевым словом friend. Функцией, дружественной классу, может быть как произвольная внешняя функция, так и составная функция другого класса, который должен быть уже определен. Например, если мы хотим перегрузить операцию вывода на экран элементов двумерного массива, определенного выше классом twomas, то нам будет нужен доступ к закрытым членам класса. Для обеспечения этого доступа в теле класса следует объявить прототип функции
friend ostream& operator << (ostream& o, twomas& d);
и определить операцию вывода с помощью внешней подпрограммы (функции):
ostream& operator << (ostream& o, twomas& d)
{
int i, j;
for(i = 1; i <= d.n; i++)
{
for(j = 1; j <= d.n; j++)
o << d(i, j) << ‘ ‘;
o << “n”;
}
return o;
}
Если класс содержит объекты другого класса в качестве полей, то его составным функциям необходим дополнительный доступ к закрытым членам этих полей. Например, в классе вектора, состоящего из n комплексных чисел
class Vectorc
{
Complex *z;
Public:
double norma();
};
составная функция norma(), возвращающая максимум абсолютных величин вещественных и мнимых компонент вектора, не имеет доступа к этим компонентам. Чтобы обеспечить этот доступ, в классе Complex следует указать функцию Vectorc::norma() как дружественную. Поскольку к моменту объявления составной функции класс
Vectorc должен быть определен, то следует указать перед определением класса Complex этот класс Vectorc как внешний (глобальный):
class Vectorc;
class Complex
{
double Re, Im;
friend double Vectorc::norma();
…
};
а затем определить класс Vectorc.
Существует возможность сделать доступными все члены класса А для каждой из составных функций класса В. Для реализации этой возможности достаточно класс B объявить дружественным для класса А. К моменту объявления класс B должен быть
определен или объявлен как внешний. Члены класса А не становятся доступными для дружественных функций класса B.
Пример. Определим класс графического окна, в которое будет выводиться график линейной функции. Линейная функция определяется как класс.
#include <graphics.h>
#include <conio.h>
class Wnd; // Прототип класса Wnd
// Класс — функция
class Func
{
// Закрытые элементы
double k, b; // y = kx + b
friend class Wnd; // Объявление дружественного класса
public: // Общедоступные элементы
Func(double k1, double b1=0): k(k1), b(b1) {} // Конструктор
};
// Класс окна
class Wnd
{
// Закрытые элементы
int xleft, xright, ytop, ybot; // Реальные координаты окна
double xmin, ymin, xmax, ymax; // Относительные координаты окна
public: // Общедоступные элементы
// Конструктор
Wnd(double x0, double y0, double x1, double y1,
int xl=0, int yt=0, int xr=639, int yb=479):
xmin(x0), ymin(y0), xmax(x1), ymax(y1),
xleft(xl), ytop(yt), xright(xr), ybot(yb) {}
Wnd& operator << (Func); // Перегрузка операции <<
};
// Перегрузка операции <<
Wnd& Wnd::operator << (Func f)
{
double xkof, ykof; // Коэффициенты перевода относительных
// координат в реальные
xkof = (xright-xleft)/(xmax-xmin);
ykof = (ybot-ytop)/(ymax-ymin);
rectangle(xleft, ytop, xright, ybot); // Рамка
line(xleft,
ytop+(ymax-ymin)*ykof/2,
xright,
ytop+(ymax-ymin)*ykof/2); // Ось х
line(xleft+(xmax-xmin)*xkof/2,
ytop,
xleft+(xmax-xmin)*xkof/2,
ybot); // Ось у
line((xright — xleft)/2 + xmin*xkof,
(ybot — ytop)/2 — (xmin*f.k+f.b)*ykof,
(xright — xleft)/2 + xmax*xkof,
(ybot — ytop)/2 — (xmax*f.k+f.b)*ykof); // Вывод функции
return (*this);
}
void main()
{
int gd=DETECT, gm;
Wnd w(-5, -3, 5, 3); // Определение окна
Func phi(1, 1); // Определение функции
initgraph(&gd, &gm, ""); // Инициализация графики
w<<phi; // Вывод функции phi в окно w
getch(); // Ожидание нажатия клавиши
closegraph(); // Закрытие графики
}
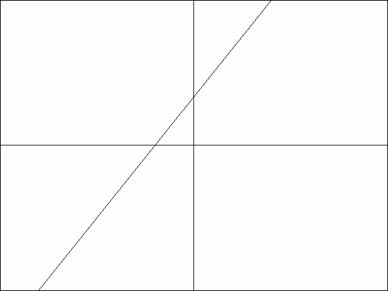
Результаты работы программы