Предположим, что сделана необходимая схематизация тел и источников, участвующих в теплообмене. Теперь для каждого компонента технологической системы или подсистемы должно быть написано и с учетом конкретных условий однозначности решено дифференциальное уравнение теплопроводности. Существуют три основные группы методов решения дифференциального уравнения теплопроводности: аналитические; численные и методы математического моделирования.

К аналитическим относятся классический метод непосредственного интегрирования, метод интегральных преобразований и метод источников. При методе непосредственного интегрирова­ния дифференциального уравнения решение выполняют одним из известных способов, например разделением переменных. Покажем применение этого метода при решении одномерной стационарной задачи. Примером, иллюстрирующим такую задачу, является определение температурного поля в инструменте при иглофрезеровании.

Схематизируя процесс, представим иголку как стержень, на торце которого действует источник теплоты, возникающий в результате преобразования механической энергии трения в тепловую (рис. 21). Граничные условия: а) на нижнем торце иголки задана плотность теплового потока, т. е. ГУ2:

б) поскольку конец проволочки заделай в массивный корпус инструмента и не успевает прогреваться, можно предположить, что на верхнем (нера

бочем) тор­це температура равна температуре окружающей среды т. е. имеем типичный случай пассивной границы с ГУ1;

в) теплоотдачей с боковой поверхности проволочки в первом приближении можем пренебречь, т. е. считать эту поверхность адиабатической.

В первом приближении можем также считать, что температура иголки при обработке достаточно широких поверхностей быстро устанавливается. Тогда дифференциальное уравнение теплопроводности приводится к виду:

.

Интегрируя это уравнение первый раз, получаем

.

Далее, разделив переменные

и интегрируя второй раз, имеем

.

Для определения постоянных интегрирования используем граничные условия (a) и (б). Тогда

.

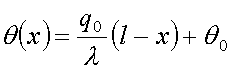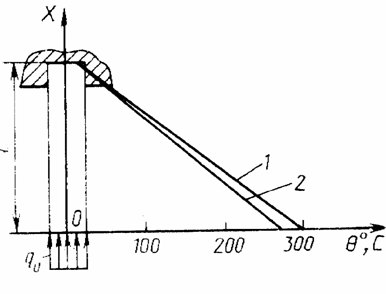
Рис.21. Распределение температур в стержне