Часто из содержательного смысла задачи линейного программирования вытекает необходимость нахождения целочисленного решения. В общем случае требования целочисленности решения являются дополнительным (и очень существенным) ограничением, которое может сильно усложнить решение задачи. В качестве примера задач целочисленного линейного программирования можно привести задачи о назначениях сотрудников и размещении оборудования.
Задача о размещении оборудования
Есть n предметов, каждый из которых обладает коэффициентом полезности (стоимостью, калорийностью, эффективностью и т.п.), массой и объемом. Общая полезность от размещения предметов равна сумме полезности отдельных предметов. Требуется при ограничениях по общей массе и объему обеспечить такое размещение предметов, при котором общий коэффициент полезности будет наибольшим.
Введем обозначения:
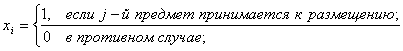
cj – коэффициент полезности j-го предмета;
aij – i-я характеристика j-го предмета;
bi – ограничение по i-й характеристике.
Тогда получим задачу целочисленного линейного программирования:
![]()
![]()
![]()
Задача о назначениях
Имеются n сотрудников, которые могут выполнять n работ, причем использование i-го сотрудника на j-м месте приносит доход cij (i,j = 1, 2,…,n). Требуется поручить каждому сотруднику выполнение определенной работы так, чтобы максимизировать суммарный доход.
Введем обозначения:
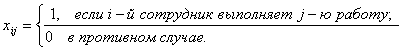
Учитывая то, что каждая работа должна быть сделана только одним сотрудником, получим:
![]()
![]()
![]() или xij =
или xij =![]()
Задачей целочисленного линейного программирования является задача:
max![]() (2.22)
(2.22)
при ограничениях
![]() (2.23)
(2.23)
![]() ≥ 0, целые, (2.24)
≥ 0, целые, (2.24)
где ![]() – n-вектор с целыми компонентами;
– n-вектор с целыми компонентами; ![]() – искомый целый n-вектор; A –
– искомый целый n-вектор; A – ![]() -матрица с целыми коэффициентами;
-матрица с целыми коэффициентами; ![]() – m-вектор с целыми компонентами;.
– m-вектор с целыми компонентами;.
Для решения поставленной задачи рассмотрим два метода: метод ветвей и границ и метод Гомори.