1. Определить главный параметр – межосевое расстояние:

где

К_а – вспомогательный коэффициент (для косозубых передач К_а = 43,для прямозубых – К_а = 49,5);

u– передаточное число редуктора или открытой передачи (cм. табл.2.3);

Т₂– вращающий момент на тихоходом валу редуктора или на приводном валу рабочей машины для открытой передачи, Н·м (см. табл. 2.3);

|/_a = b₂/a_w – коэффициент ширины венца колеса (для шестерни, расположенной симметрично от­носительно опор в проектируемых нестандартных одноступен­чатых цилиндрических редукторах |/_a = 0,28.. .0,36; для шестер­ни, консольно расположенной относительно опор в открытых передачах |/_а = 0,2. ..0,25);

[σ]_Н – допускаемое контактное напряжение колеса с ме­нее прочным зубом или среднее допускаемое контактное напряжение, Н/мм²;

К_Hβ – коэффициент неравномерности нагрузки по длине зуба. Для прирабатывающихся зубьев К_Нβ = 1.

Полученное значение межосевого расстояния (a_w)для нестан­дартных передач округлить до ближайшего значения из ряда нормальных линейных размеров (табл. 2.10).

Таблица 2.10 Нормальные линейные размеры (ГОСТ 6636 – 69), мм

Ряд	Размеры
Ra10	40; 50; 63; 80; 100; 125; 160; 200; 250; 320; 400; 500; 630; 800
Ra20	40; 45; 50; 56; 63; 71; 80; 90; 100; 110; 125; 140; 160; 180; 200; 220; 250; 280; 320; 360; 400; 450; 500; 560; 630; 710
Ra40	40; 42; 45; 48; 50; 53; 56; 60; 63; 67; 71; 75; 80; 85; 90; 95; 100; 105; 110; 120; 125; 130; 140; 150; 160; 170; 180; 190; 200; 210; 220; 240; 250; 260; 280; 300; 320; 340; 360; 380; 400; 420; 450; 480; 500;530; 560; 600; 630; 670; 710; 750; 800; 850; 900

2. Определить модуль зацепления:

m = ,

где

К_m– вспомогательный коэффициент (для косозубых передач К_m = 5,8 , для прямозубых К_m = 6,8;

d₂ = (2 a_wu) / (u + 1) – делительный диаметр колеса, мм;

b₂ = _aa_w – ширина венца колеса, мм;

Полученное значение модуля (m) округлить в большую сторону до стандартного из ряда чисел. При выборе модуля 1-й ряд следует предпочитать 2-му (табл. 2.11).

Таблица 2.11 Модули цилиндрических и конических зубчатых колес (ГОСТ 9563-60)

Ряд	Модули
1	1,00; 1,25; 1,50; 2,00; 2,50; 3,00; 4,00; 5,00; 6,00; 8,00
2	1,125; 1,375; 1,750; 2,250; 2,750; 3,500; 4,500; 5,500; 7,000; 9,000

В силовых зубчатых передачах при твердости колес < 350 НВ принять m1 мм; при твердости одного из колес  45 HRC_э принять m1,5 мм.

В открытых передачах из-за повышенного изнашивания зубьев расчетное значение модуля mуве­личить на 30 %.

1.  Определить угол наклона зубьев (β_min)для косозубых передач:

β_min= arcsin

В косозубых передачах угол наклона зубьев принимают: β = 8… 16°, но из-за роста осевых сил (F_a)в зацеплении желательно получить его меньшие значения, изменяя значение модуля и ширину колеса (b₂)

2. Определить суммарное число зубьев шестерни и колеса:

для прямозубых колес      z_Σ = z₁+z₂= 2 a_w/ m;

для косозубых колес       z_Σ = z₁+z₂= (2 a_wcosβ_{min )}/ m.

Полученное значение z_Σ округлить в меньшую сторону до целого числа.

3. Уточнить действительную величину угла наклона зубьев для косозубых передач (точность вычисления угла β до пятого знака после запятой):

β = (arcos z_Σ m) / (2a_w).

4. Определить число зубьев шестерни:

z_t =

Значение z₁ округлить до ближайшего целого числа. Из условий уменьшения шума и отсутствия подрезания зубьев рекомендуется: z₁ 18.

5. Определить число зубьев колеса:

z₂ = z_Σ – z₁.

6. Определить фактическое передаточное число (u_ф) и проверить его отклонение (Δu) от заданного (u):

u_ф = z₂ / z₁;           Δ_u= .

При невыполнении нормы отклонения передаточного числа (Δ_u) пересчитать z_tи  z₂.

7. Определить фактическое межосевое расстояние:

для прямозубых передач  a_w = (z₁ + z₂) m / 2;

для косозубых передач    a_w = (z₁ + z2) m (2 cos β).

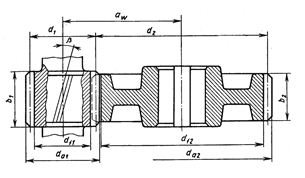
Рис. 2.2. Геометрические параметры цилиндрической зубчатой передачи

1. Определить основные геометрические параметры пере­дачи (рис. 2.2). Точность вычисления делительных диаметров колес до 0,1 мм; значение ширины зубчатых венцов округляют до целого числа по нормальным линейным размерам (см. табл. 2.12).

Таблица 2.12 Геометрические параметры передачи, мм

Параметр		Шестерня		Колесо
		прямозубая	косозубая	прямозубое	косозубое
Диаметр	делительный	d1 = m z1	d1 = m z1 / cosβ	d2 = m z2	d2 = m z2 / cos β
	вершин зубьев	da1  = d1 + 2m		da2 = d2 + 2 m
	впадин зубьев	df1 = d1 – 2,4m		df2 = d2 – 2,4 m
Ширина венца		b1 = b2 + (2…4)		b2 = ψa aw