В связи с развитием вычислительной техники все более широкое применение при описании тепловых процессов в технологических системах находят численные методы решения дифференциального уравнения теплопроводности. Они в своей основе являются приближенными

методами интегрирования дифференциальных уравнений. Как всякие приближенные вычислительные методы, они позволяют учесть больше особенностей конкретного процесса, чем при аналитическом подходе, поскольку не связаны с чисто математическими трудностями, возникающими при аналитических способах решения.

Вместе с тем конкретность условий, для которых получен результат вычисления, делает численный анализ справедливым только для этих условий (конкретный режим, конкретный вид зависимости ^ (0), конкретная конфигурация твердого тела и т. д.). Поэтому единичный результат численного счета не позволяет непосредственно выявить обобщенные закономерности, характеризующие влияние того или иного параметра процесса на температурное поле и теплообмен в технологической подсистеме, как это можно сделать на основании формул, полученных аналитическим путем. Для того чтобы установить эти закономерности, необходимо выполнить численное решение несколько раз при различных значениях интересующего нас параметра, а затем каким-либо способом аппроксимировать результаты машинного счета.

При решении задач технологической теплофизики применяют:

метод конечных разностей, метод конечных элементов и метод граничных элементов. Не углубляясь в технику вычислений и методику их осуществления на ЭВМ, поскольку это выходит за рамки данного пособия, рассмотрим принципиальные особенности каждого из упомянутых выше методов на примере решения сравнительно простых задач технологической теплофизики.

Метод конечных разностей. Этот метод основан на замене истинных значений производных приближенными значениями в некоторых точках, называемых узлами. Узлы являются центрами элементов конечной длины, на которые разбивается твердое тело, участвующее в теплообмене.

Метод конечных элементов. Разбиение твердых тел на одинаковые по размеру элементарные объемы (рисунок 23), а времени — на одинаковые промежутки, как это делается в методе конечных разностей, вызывает для более или менее сложных случаев теплообмена в технологиче

ских подсистемах столь большой объем вычислительной работы, что процесс счета оказывается очень длительным и дорогостоящим, а подчас с ним не справляются даже мощные ЭВМ. Желание существенно уменьшить объем вычислений привело к разработке метода конечных элементов (МКЭ). Метод конечных элементов учитывает тот факт, что в любой конкретной задаче, в том числе технологической, разные участки системы твердых тел представляют для теории и практики различный интерес. Например, сведения о температуре контактных поверхностей и прилежащих к ним участков инструмента, обрабатываемой заготовки или соприкасающихся деталей машин, как правило, представляют больший интерес, чем температура участков и поверхностей, удаленных от зоны контакта. Следовательно, приконтактные объемы твердых тел в технологической подсистеме должны быть изучены с большей степенью детализации, чем удаленные, они должны быть при численном методе решения дифференциального уравнения теплопроводности разбиты на конечные элементы более мелкие, чем удаленные участки технологической зоны. Метод конечных элементов позволяет осуществлять различную детализацию решения в разных областях изучаемого объекта, причем могут быть использованы элементарные объемы, различные не только по величине, но и по конфигурации.

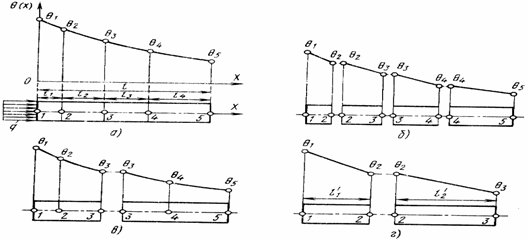
Рис.23. Разбиение стержня при использовании метода конечных элементов