Рассмотрим другой класс нейронных сетей, называемый нейронными сетями с радиально-базисными функциями (РБФ).

Сети РБФ имеют ряд преимуществ перед рассмотренными многослойными сетями прямого распространения, хотя их структура и соответствует приведенной на рис. 2.5. Во-первых, они моделируют произвольную нелинейную функцию с помощью всего одного промежуточного слоя, тем самым избавляя разработчика от необходимости решать вопрос о числе слоев. Во-вторых, параметры линейной комбинации в выходном слое можно полностью оптимизировать с помощью хорошо известных методов линейной оптимизации, которые работают быстро и не испытывают трудностей с локальными минимумами, так мешающими при обучении с использованием алгоритма обратного распространения ошибки. Поэтому сеть РБФ обучается очень быстро – на порядок быстрее, чем с использованием алгоритма ОР.

Недостатки сетей РБФ: данные сети обладают плохими экстраполирующими свойствами и получаются весьма громоздкими при большой размерности вектора входов.

На рис.2.22 представлена структурная схема нейронной сети с радиальными базисными функциями.

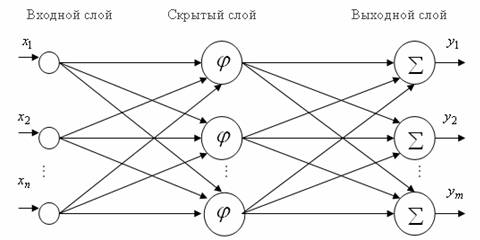
  Рис.2.22. Сеть с радиальными базисными функциями

Нейронная сеть радиальных базисных функций содержит в наиболее простой форме три слоя: обычный входной слой, выполняющий распределение данных образца для первого слоя весов; слой скрытых нейронов с радиально симметричной активационной функцией, каждый -й из которых предназначен для хранения отдельного эталонного вектора в виде вектора весов ; выходной слой. Для построения сети РБФ необходимо выполнение следующих условий.

Во-первых, наличие эталонов, представленных в виде весовых векторов нейронов скрытого слоя. Во-вторых, наличие способа измерения расстояния входного вектора от эталона. Обычно это стандартное евклидово расстояние. В-третьих, специальная функция активации нейронов скрытого слоя, задающая выбранный способ измерения расстояния. Обычно используется функция Гаусса, существенно усиливающая малую

разницу между входным и эталонным векторами. Выходной сигнал эталонного нейрона скрытого слоя – это функция (гауссиан) только от расстояния  между входным и эталонным векторами:

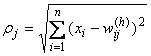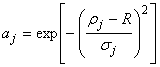;     ;    ,      (2.55)

где  – активационный уровень нейрона  скрытого слоя;  – входной вектор;  – весовой вектор -го эталонного нейрона скрытого слоя; ,  – параметры активационной функции;  – число эталонов – нейронов скрытого слоя.

Таким образом, выходной сигнал шаблонного нейрона – это функция только от расстояния между входным вектором  и сохраненным центром :

.                                                    (2.56)

Обучение слоя образцов-нейронов сети подразумевает предварительное проведение кластеризации для нахождения эталонных векторов и определенных эвристик для определения значений .

Нейроны скрытого слоя соединены по полносвязной схеме с нейронами выходного слоя, которые осуществляют взвешенное суммирование:

;               ,               (2.57)

где – центры; – отклонения радиальных элементов.

Для нахождения значения весов  от нейронов скрытого к выходному слою используется линейная регрессия.

В общем случае активационные функции нейронов скрытого слоя могут отражать законы распределения случайных величин (вероятностные нейронные сети) либо характеризовать различные аналитические зависимости между переменными (регрессионные нейронные сети).

К недостаткам сетей РБФ можно отнести то, что заранее должно быть известно число эталонов, а также эвристики для построения активационных функций нейронов скрытого слоя.

В моделях РБФ могут быть использованы различные способы измерения расстояния между векторами, а также функции активации нейронов скрытого слоя.