Контекстно-свободные грамматики традиционно служат основой для синтаксического анализа компиляции. Описание входного языка включает пра­вила синтаксиса, в соответствии с которыми порождаются тексты программ. Каждому синтаксическому правилу в КС-грамматике соответствует правило вывода (продукция) грамматики. Поэтому последовательность правил вывода грамматики, которые применяются для порождения текста программы, опре­деляет ее структуру. Выводов некоторой цепочки w в грамматике G в общем случае может быть достаточно много. Это происходит в силу того, что если некоторая промежуточная цепочка вывода содержит более чем одно вхожде­ние нетерминального символа, то правила подстановки могут применяться, в принципе, к любому вхождению нетерминального символа. Если изменить лишь порядок применения правил, а сами правила будут использоваться те же, то, очевидно, будет получен другой вывод, но заключительная терминальная це­почка и ее определяемая выводом синтаксическая структура останутся неиз­менными. Обычно множество выводов КС-грамматики ограничивается, и рассматриваются не все ее возможные выводы, а лишь так называемые левос­торонние или правосторонние выводы.

Определение 3.1.1. Вывод в КС-грамматике называют левосторонним (пра­восторонним), если правила вывода применяются к самому левому (правому) вхождению нетерминального символа каждой цепочки вывода.

Пример 3.1.1. Рассмотрим КС-грамматику G = <N, Т, Р, S>, у которой

N = {E,R,F},T = {i,+,*,),(},S = {E},

Р = {    1. Е  E+R

                           2. E R

                           3. R R*F

                           4. R F

                           5. F (E)

                           6. F i}.

Данная КС-грамматика порождает арифметические выражения, построен­ные из идентификаторов (в грамматике идентификатору соответствует терми­нальный символ i), знаков арифметических операций + и *, скобок ( и).

Для терминальной цепочки i+i*i построим ее левосторонний и правосто­ронний выводы:

а) левосторонний вывод:

     1            2             4            6           3               4               6              6

E  E+R  R+R  F+R  i+R  i+R*F  i+F*F  i+i*F  i+i*i.

б) правосторонний вывод:

     1             3                6                4                6              2                4             6

E  E+R  E+R*F  E+R*i  E+F*i   E+i*i   R+i*i   F+i*i  i+i*i.

Получение синтаксической структуры программы в форме шагов вывода не совсем удобно — в выводе не просматривается явно структура программы. Более наглядным является представление структуры программы в виде дерева вывода (дерева синтаксического разбора).

Под деревом синтаксического разбора будем понимать конечный неориен­тированный граф, обладающий свойствами[6]:

· у него имеется одна вершина, в которую не входит ни одна дуга; эту вершину будем называть корнем дерева, корень дерева соответ­ствует начальному символу грамматики — аксиоме;

· в каждую из его остальных вершин входит лишь одна дуга; верши­ны, не имеющие выходящих из них дуг, называются заключительными вершинами дерева или листьями, в КС-грамматике им соответствуют терминальные символы грамматики; не заключительным вершинам де­рева соответствуют нетерминальные символы грамматики;

· он не содержит контуров.

Более формально, дерево разбора в КС-грамматике G = <N, Т, Р, S> — это упо­рядоченное дерево, каждая вершина которого помечена символом X Т  N.

Если внутренняя вершина помечена символом А, а ее прямые потомки — символами X₁, X₂, …, Х_r, то А  Х₁, Х₂, …, Х_r — правило грамматики G. Постро­ение синтаксического дерева D_n по выводу S = ₀, ₁,…,_n осуществляется следующим образом:

1) при m = 0 D₀ состоит из одной вершины, помеченной символом S – аксиома грамматики G;

2) пусть при 0mn для вывода S = ₀, ₁,…,_n построено дерево D_m и _m = = x₁Ax₂, _m+1 = x₁x₂, и А   — правило из Р, = X₁X₂…X_r. В дереве D_m символы цепочки _m являются метками его листьев, выписанных слева на право. Тогда дерево вывода D_m+1 с цепочкой листьев _m+1 строиться путем добавления новых листьев с метками X₁, X₂, …, X_r и соответствующих ребер;

3) дерево D_n – искомое дерево для вывода S = ₀, ₁,…,_n.

В случае полного вывода цепочка _n состоит из терминальных символов, поэтому ни вывод, ни дальнейшие построения дерева вывода не возможны.

На рис. 3.1. показано дерево синтаксического разбора цепочки i+i*i для грам­матики из примера 3.1.1. Левостороннему выводу цепочки соответствует об­ход ее дерева вывода сверху вниз и слева направо. Аналогично определяется и правосторонний вывод, только ориентацию пути обхода дерева необходимо поменять на обратную.

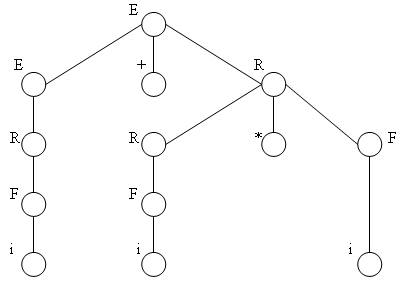
Рис. 3.1. Дерево синтаксического разбора цепочки i+i*i для грамматики из примера 3.1.1

Определение 3.1.2. КС-грамматика называется однозначной, если для неко­торой цепочки (NТ)⁺ существует только одно дерево вывода. В против­ном случае грамматика называется неоднозначной.

Необходимо отметить, что однозначность или неоднозначность, это свой­ство грамматики G, а не языка L(G). В общем случае один и тот же язык можно описать с помощью бесконечного множества порождающих его грамматик. Для практических целей имеет смысл рассматривать лишь однозначные граммати­ки, которые обеспечивают однозначную семантическую интерпретацию про­граммы и соответственно получение машинной программы.

Например, для языка арифметических выражений из примера 3.1.1. грам­матика с правилами Е  Е+Е | Е*Е | i неоднозначна, так как цепочка i+i*i имеет два дерева вывода (рис. 3.2.).

Поэтому такая грамматика не может служить основой для выполнения син­таксического анализа.

Определение 3.1.3. КС-грамматика G называется:

а)  леворекурсивной, если в ней имеются выводы вида

XX, где XN, V⁺;

б) праворекурсивной, если в ней имеются выводы вида

XX, где XN, V⁺;

в) самовставляющей, если она имеет выводы вида

XX, где XN и ,V⁺.

КС -грамматика G называется рекурсивной, если имеет место хотя бы один из случаев а)  —  в).

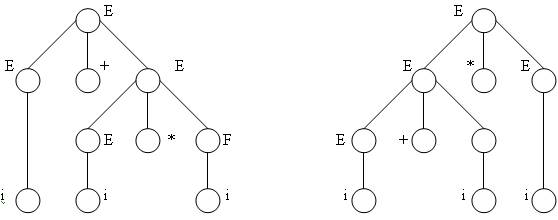
Рис. 3.2. Неоднозначные деревья вывода

В общем случае любая КС-грамматика, описывающая язык программи­рования, является рекурсивной. Важным является выявление вида рекурсии при использовании того или иного метода синтаксического разбора. Различ­ные методы построения дерева синтаксического разбора допускают в грамма­тике, как правило, лишь один вид рекурсии. Задачу синтаксического разбора можно сформулировать следующим образом: для заданного предложения a₁, a₂…a_n T и грамматики G построить треугольник и попытаться заполнить его внутреннюю часть деревом синтаксического разбора [13]:

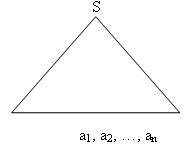
В принципе, не имеет значения то, каким образом будет заполняться внут­ренняя часть треугольника. На рис. 3.3. изображены три наиболее используе­мых способа заполнения треугольника.

Стратегия синтаксического разбора, изображенная на рис. 3.3, а называется разбором сверху вниз. Так как программа может состоять из многих тысяч пред­ложений, методы, требующие размещения в оперативной памяти все­го предложения в общем случае неприемлемы. Поэтому на практике применяются методы, заполняющие треугольник, используя часть предложе­ния. Очевидный способ разбора предложения по частям — перебирать слова по одному слева направо в их естественной последовательности. При этом ис­пользуются две основные стратегии заполнения треугольника разбора: сверху вниз и слева направо (рис. 3.3, б) или снизу вверх и слева направо (рис. 3.3, в).

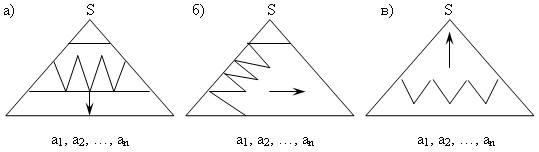
Рис. 3.3. Основные способы построения синтаксического дерева

Выбор стратегии синтаксического разбора для конкретной КС-граммати­ки, в общем случае, обуславливает быстроту его выполнения. В настоящее время разработано и используется на практике большое количество алгоритмов раз­бора. Каждый из них использует ту или иную стратегию разбора и в большин­стве случаев накладывает различные ограничения на правила КС-грамматик, т.е. исходная КС-грамматика, прежде чем она может быть использована в каче­стве основы синтаксического разбора, должна быть подвергнута определен­ным преобразованиям. Эти преобразования в конечном итоге обеспечивают:

· однозначность, детерминированность грамматического разбора;

· устраняют лишние шаги в дереве разбора;

· простые эмпирические критерии выбора продукции из множества альтернативных.

Ниже будут рассмотрены такие преобразования КС-грамматик, которые не затрагивают главного — способности порождать преобразованной КС-грам­матикой того же языка, что и исходная КС-грамматика.