Определение. Если е = {v, w} – ребро графа, то вершины v, w называются концами ребра е; в этом случае также говорят, что ребро е соединяет вершины v, w.

Определение. Если е = {v, w} – дуга орграфа, то вершина v называется началом, а вершина w – концом дуги е; в этом случае также говорят, что дуга е исходит из вершины v и заходит в вершину w.

Между элементами множества вершин и множества ребер определено отношение инцидентности. Говорят, что ребро е инцидентно вершинам v, w, если оно соединяет эти вершины и наоборот, каждая из вершин v, w инцидентна ребру е.

Определение. Две вершины называются смежными, если существует ребро, концами которого они являются. Два ребра называются смежными, если они имеют общую вершину.

Определение. Степенью вершины v графа G называется число d(v) ребер графа, которым инцидентна эта вершина.

Определение. Вершина, локальная степень которой равна 0, называется изолированной; степень которой равна 1 – висячей.

Замечание. В случае неориентированного псевдографа  обычно считается, что  вклад каждой петли, инцидентной некоторой вершине v, равен 2 (тогда как вклад любого другого ребра, инцидентного вершине v, равен 1).

Определение. Полустепенью исхода (захода) вершины v орграфа D называется число d⁺(v) (d ^-(v)) дуг орграфа D, исходящих из вершины v (заходящих в вершину v).

Замечание. В случае ориентированного псевдографа вклад каждой петли, инцидентной некоторой вершине v, равен 1, как в d⁺(v), так и в d ^-(v).

Количество вершин  и ребер в графе G обозначим соответственно через n(G)  и m(G), а количество вершин и дуг в орграфе D – через n(D) и  m(D).

Утверждение. Для любого псевдографа G выполняется равенство

Утверждение. Для любого ориентированного псевдографа D выполняется равенство

Пример 69.

Найти локальные степени графа (рис. 3.1) и орграфа (рис. 3.2).

Решение.

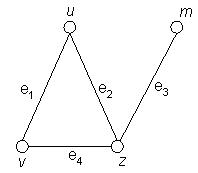
Рис. 3.1. Граф для примера 69

d (u) = 2;

d (v) = 2;

d (z) = 3;

d (m) = 1.

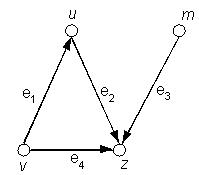
Рис. 3.2. Орграф для примера 69