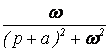Рассмотрим еще два свойства преобразования Лапласа, которые также относятся к основным. Они устанавливают связь между изображением и оригиналом и изображениями её производной  и интеграла .

Предположим, что f(t) дифференцируемая при t > 0, причем . Тогда сама . В самом деле, так как существует , то  – непрерывна при , кроме того, поскольку , то .

Пусть f(t)  F(p). Применяя (3.21) к интегрированию по частям, получим:

f(t) .

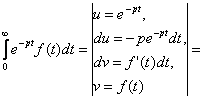
Итак,

                                                   (3.22)

где под f(0) понимаем правое предельное значение , и при Rep = s >s₀

Если , то

                                                         (3.23)

Методическое руководство

Соотношение (3.22) говорит о том, что дифференцированию оригинала f(t) в множестве оригиналов D, соответствует операция умножения на p изображения F(p) и вычитания значения оригинала f(0) в области изображений.

Соответствия (3.22) и (3.23) обобщаются:

                     (3.24)

Продолжая этот процесс, записываем, что:

                                (3.25)

Пример 1

Пусть . Найти изображение .

Решение. Имеем:

,

откуда .

Свойства (3.24) и (3.23) играют фундаментальную роль при применении преобразования Лапласа к решению дифференциальных уравнений и их систем.

Так, если предположить существование для функции f(t) производных высших порядков и принадлежность их к классу D, то легко установить их изображения, зная изображение первой производной, интегрируя соответственно нужное число раз по частям. Следует отметить, что формула (3.25) выглядит особенно просто при нулевых начальных условиях: ,

                                                       (3.26)

Пример 2

Дано:  найти изображение .

Решение. Так как

и                                     ,

то                                 .

Изображение интеграла найдем, введя функцию , так как   будет функцией-оригиналом.

Пусть     и   .   Тогда

   или   F(р) = рФ(р) – (0),   то   Ф(р) = .

Однако , поэтому .

Итак,

.                                                    (3.27)

Пример 3

Известно, что . Найти изображение функций .

Решение. Так как , то .

При изучении основ преобразования Лапласа рекомендуется записывать получаемые соответствия в таблицу соответствия «оригинал-изображение» (табл. 3.1).

Таблица 3.1