Рассмотрим некоторые важные типы графов.

Определение. Граф, у которого множество ребер пусто, называется вполне несвязным (или пустым) графом. Вполне несвязный граф обозначают  N_n.

Заметим, что у вполне несвязного графа все вершины изолированы.

Рис. 3.10. Пример пустого графа

Определение. Простой граф, в котором любые две вершины смежны, называется полным. Полный граф обозначают  К_n.

Пример 74.

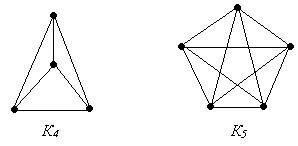
Заметим, что для полного графа выполняется равенство , где m – число ребер, n – число вершин графа.

Определение. Граф, у которого все вершины имеют одну и ту же локальную степень n, называется регулярным (или однородным) степени n.

Регулярные графы степени 3 называются кубическими (или трехвалентными).

Пример 75.

Известным примером кубического графа является граф Петерсона (рис. 3.11).

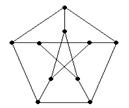
Рис. 3.11. Граф Петерсона

Среди регулярных графов особенно интересны так называемые платоновы графы – графы, образованные вершинами и ребрами пяти правильных многогранников – Платоновых тел: тетраэдра, куба, октаэдра, додекаэдра и икосаэдра.

Пример 76.

На рис. 3.12 приведен граф, соответствующий кубу.

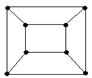
Рис. 3.12. Граф, соответствующий кубу

Определение. Допустим, что множество вершин графа G можно разбить на два непересекающихся подмножества V₁ и V₂ так, что каждое ребро в G соединяет какую-нибудь вершину из V₁ с какой-нибудь вершиной из V₂, тогда данный граф называется двудольным.

Двудольный граф можно определить и по-другому – в терминах раскраски его вершин двумя цветами, скажем красным и синим. При этом граф называется двудольным, если каждую его вершину можно окрасить красным или синим цветом так, чтобы каждое ребро имело один конец красный, а другой – синий.

Определение. Если в двудольном графе каждая вершина из V₁ соединена с каждой вершиной из V₂, то граф называется полным двудольным.

Обозначение. К_{m. n.}

Заметим, что граф К_{m. n} имеет ровно m + n вершин и mn ребер.

Пример 77.

На рис. 3.13 изображены двудольные графы.

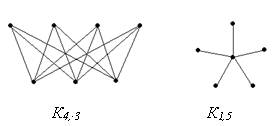
Рис. 3.13. Двудольные графы

Определение. Объединением графов  называется граф

Определение. Пересечением графов , где , называется граф

Определение. Соединением графов G₁ и G₂ является новый граф, у которого V=V₁V₂ , а множеством ребер являются все ребра первого и второго графа и ребра, соединяющие между собой каждую вершину первого графа с первой вершиной второго графа.

Определение. Граф называется связным, если его нельзя представить в виде объединения двух графов, и несвязным в противном случае.

Очевидно, что всякий несвязный граф можно представить в виде объединения конечного числа связных графов – каждый из таких связных графов называется компонентой связности графа.

Определение. Связный регулярный граф степени 2 называется циклическим графом. Обозначается  С_n (рис. 32).

Определение. Соединение графов N₁ и C_n-1 (n3) называется колесом с n вершинами. Обозначается  W_n (рис. 3.14).

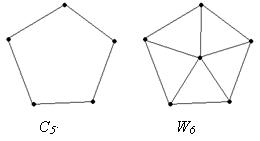
Рис. 3.14. Пример колеса

Пример 78.

Определение. Дополнением простого графа G называется простой граф с множеством вершин V(G), в котором две вершины смежны тогда и только тогда, когда они не смежны в исходном графе.

Обозначение.

Другими словами, дополнением графа является граф, содержащий все вершины исходного графа и только те ребра, которых не хватает исходному графу для того, чтобы он стал полным.

Определение. Подграфом графа G называется граф, все вершины и ребра которого содержатся среди вершин и ребер графа G. Подграф называется собственным, если он отличен от самого графа.