При расчете напряжений от изгиба сверло рассматривается как консольная балка, нагруженная неуравновешенной радиальной силой Р. Расчет напряжений изгиба в произвольной точке любого сечения можно производить по формуле:

,                                                                                            (3.8)

где М – изгибающий момент в произвольном сечении В-В (рис.3.12), , где Р – равнодействующая сила;  — длина вылета сверла;  — расстояние от заделки  до рассматриваемого сечения;  — координаты рассматриваемой точки;  — угол разворота рассматриваемого сечения относительно сечения А-А заделки;  и  — главные моменты инерции сечения.

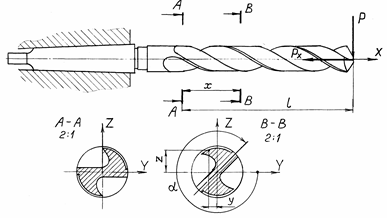
Рис. 3.12. К расчету сверл на прочность

Продольный изгиб наблюдается при нагружении сверла осевой силой , при этом критические напряжения равны

.                                                                                                                (3.9)

Расчет сверл на продольный изгиб производится по зависимости

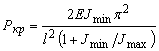,                                                                                           (3.10)

где Е – модуль упругости при растяжении;  и  — наибольший и наименьший моменты инерции сечения сверла.

Для сверл с коническим хвостовиком целесообразно расчетным путем определить размеры конуса, чтобы не допустить проворота сверла в коническом отверстии оправки.

Определим максимальный крутящий момент, который может передать конус хвостовика сверла, т.е. момент, по достижении которого будет наблюдаться  проскальзывание.

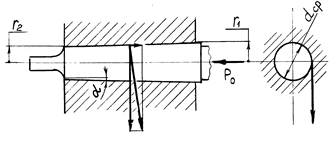
Рис. 3.13. К расчету хвостовика спирального сверла

Осевое усилие  сжимает две конические поверхности (рис.3.13), и между ними возникает трение, момент которого определяется по формуле

,                                                                                                                (3.11)

где  — коэффициент между трущимися поверхностями;  — среднее удельное давление; F – площадь соприкасающихся поверхностей;  — приведенный радиус трения соприкасающихся поверхностей:

.                                                                                                      (3.12)

Расчетный крутящий момент , исходя из максимального крутящего момента , будет равен

,                                                                                                              (3.13)

где  — коэффициент запаса сцепления.

  Для устранения проскальзывания необходимо, чтобы

.                                                                                   (3.14)

Удельное давление определяется по зависимости

,                                                                                                               (3.15)

где  — половина угла при вершине конуса.

Тогда

,                                                                                                         (3.16)

а с учетом погрешности изготовления конических поверхностей

,                                                                                       (3.17)

где  — суммарная погрешность изготовления угла  конических поверхностей, измеряемая в минутах.

Отношение  к  для конструкционных сталей можно принять приблизительно равным , однако, с увеличением износа это соотношение может достигать . Тогда из (3.17) получим:

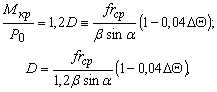
или окончательно

.                                                                                        (3.18)