Чтобы в реальной колебательной системе получить незатухающие колебания, надо компенсировать потери энергии. Такая компенсация возможна с помощью какой-либо периодически действующей силы, изменяющейся по гармоническому закону:
![]() .
.
Дифференциальное уравнение вынужденных механических колебаний имеет вид:
![]() . (3.6)
. (3.6)
Решением уравнения (3.6) является сумма общего решения однородного уравнения (3.5)
![]()
и частного решения
 ,
,
где
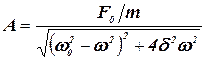 – (3.7)
– (3.7)
амплитуда вынужденных колебаний;
 – (3.8)
– (3.8)
начальная фаза вынужденных колебаний.
Слагаемое (3.5) играет существенную роль только в начальной стадии процесса (при установлении колебаний) до тех пор, пока амплитуда вынужденных колебаний не достигнет значения, определяемого равенством (3.7). В установившемся режиме вынужденные колебания происходят с частотой w и являются гармоническими; амплитуда и фаза колебаний, определяемые выражениями (3.7) и (3.8), также зависят от w.