Проектирование многих технических объектов связано с необходимостью решения дифференциальных уравнений в частных производных. Приведем ДУЧП, используемые при моделировании, например, современных летательных аппаратов /4/.
Первая важная задача проектирования летательного аппарата – определение прочности узлов и элементов конструкции при различных видах нагружения. Поэтому исследование напряженного состояния деталей конструкции и связанные с ним расчеты на прочность относятся к наиболее ответственным в самолетостроении.
Напряженное состояние деталей конструкции в зависимости от геометрии моделируемого узла описывается различными ДУЧП, однако любое из них может быть получено из общего квазигармонического уравнения (3.1):
![]() (3.1)
(3.1)
где x,y,z – пространственные координаты; φ – искомая непрерывная функция; Kx, Ky, Kz — коэффициенты; Q – внешнее воздействие.
Вторая важная задача проектирования летательного аппарата – изучение его аэродинамических свойств. Решение этой задачи связано с исследованием процессов обтекания газом поверхностей произвольной формы. Наиболее общими уравнениями, описывающими этот процесс, являются уравнения Навье-Стокса, которые для декартовой системы координат имеют вид (3.2):
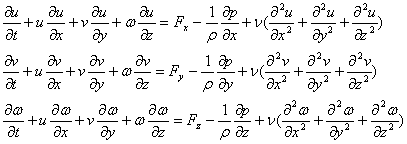 (3.2)
(3.2)
где u, v, ω – проекции вектора скорости; Fx, Fy, Fz - проекции вектора силы на оси координат; ρ – плотность; p — давление; ν = μ/ρ (μ – коэффициент вязкости); t – время.
Третья важная задача проектирования летательного аппарата – расчет тепловых режимов работы деталей и узлов конструкции. Температурное поле в сплошной среде описывается уравнением теплопроводности (3.3):
![]() (3.3)
(3.3)
где T – температура; λ – коэффициент теплопроводности; Q – источник теплоты внутри тела.
Перечисленные выше уравнения имеют множество решений. Для получения единственного решения необходимо задавать краевые условия, то есть сведения об искомых непрерывных функциях на границах рассматриваемых областей – граничные условия, а в случае нестационарных задач – значения этих же функций в начальный момент времени – начальные условия. Исходное дифференциальное уравнение в частных
производных вместе с краевыми условиями носит название дифференциальной краевой задачи и представляет собой математическую модель исследуемого объекта.
Точное решение краевых задач удается получить лишь для немногих частных случаев. Поэтому общий способ их решения, в том числе и в САПР, АРМ, заключается в использовании различных приближенных моделей. В настоящее время наиболее широкое распространение получили модели на основе интегральных уравнений и модели на основе метода сеток.
Модели на основе интегральных уравнений создаются в результате преобразований исходных дифференциальных уравнений в частных производных в эквивалентные интегральные уравнения.
Модели на основе метода сеток создаются в результате аппроксимации искомой непрерывной функции совокупностью приближенных значений, рассчитанных в некоторых точках области – узлах. Совокупность узлов, соединенных определенным образом, образует сетку. Наиболее часто в составе САПР, АРМ используются два метода сеток: метод конечных элементов (МКЭ) и метод конечных разностей (МКР).
Метод конечных элементов (МКЭ) является одним из наиболее популярных методов решения краевых задач в САПР. В математическом отношении метод относится к группе вариационно-разностных. Строгое доказательство таких важных свойств, как устойчивость, сходимость и точность метода, приводится в соответствующих разделах математики и часто представляет собой непростую проблему.
Метод конечных разностей (МКР) начал развиваться раньше МКЭ и является старейшим методом решения краевых задач. Алгоритм его состоит из этапов, традиционных для метода сеток:
Этап 1. Построение сетки в заданной области;
Этап 2. Замена дифференциального оператора в исходном дифференциальном уравнении разностным аналогом;
Этап 3. Решение полученной системы алгебраической системы уравнений.
Студенты специальности 2204 достаточно подробно знакомятся с этими методами в соответствующих курсах математики /9/, /10/. Напомним основную идею методов на примере второго этапа МКР.
Замена дифференциального оператора разностным аналогом
Пусть непрерывная функция φ(x) определена на отрезке [x0,xN+1] и описывается дифференциальным уравнением
![]()
где А – константа; задано также граничное условие φ(0) = 1 и выполнена дискретизация отрезка [x0,xN+1] с шагом h. Заменим дифференциальный оператор Lφ = dφ/dx разностным
Lh+ = [φ(x+h)-φ(x)]/h, (3.4)
где Lh+ - правая разностная производная. Подставив ее в дифференциальное уравнение, получим разностное уравнение
[φ(x+h)-φ(x)]/h + A φ(x) = 0,
записав которое для каждой точки отрезка [x0,xN+1], получим систему алгебраических уравнений. Решение такой системы дает возможность определить значения искомой функции φ(x) во всех точках интервала [x0,xN+1].
Для аппроксимации дифференциального оператора разностным можно использовать дифференциальный оператор
Lh- = [φ(x)-φ(x-h)]/h, (3.5)
где Lh- - левая разностная производная. Аналогично можно аппроксимировать и центральной разностной производной:
Lh0 = [φ(x+h)-φ(x-h)]/(2h). (3.6)
Удобным геометрическим изображением схем построения разностных производных являются шаблоны /4/. На рис. 3.1 представлены шаблоны для одномерной области.
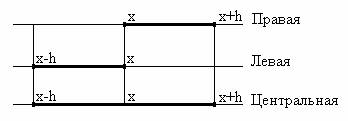
Рис. 3.1. Шаблоны одномерной области
Для аппроксимации двумерной области наибольшее распространение получили шаблоны «прямоугольник» и «крест» (рис. 3.2).
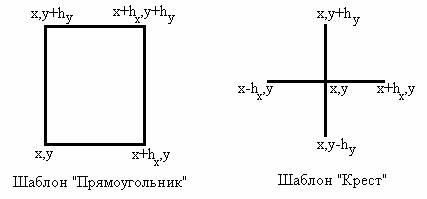
Рис. 3.2. Шаблоны двумерной области
Шаблону типа «Прямоугольник» соответствует разностный аналог
dφ/dx ≈ 0.5[φ(x+hx,y)-φ(x,y)]/hx + 0.5[φ(x+hx,y+hy)-φ(x,y+hy)]/hx;
dφ/dy ≈ 0.5[φ(x,y+hy)-φ(x,y)]/hy + 0.5[φ(x+hx,y+hy)-φ(x+hx,y)]/hy.
Шаблону типа «Крест» соответствует разностный аналог
dφ/dx ≈ [φ(x+hx,y)-φ(x-hx,y)]/2hx;
dφ/dy ≈ [φ(x,y+hy)-φ(x,y-hy)]/2hy;
где hx и hy – шаги сетки в направлениях x и y.
Для произвольного внутреннего узла (x,y) вторые производные по координатам аппроксимируются разностными аналогами λx λy c помощью шаблона «Крест»:
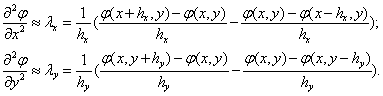
Введя обозначения φ(x+hx,y) = φi+1,j; φ(x,y-hy) = φi,j-1; b и т.д. разностные аналоги λx и λy можно записать в более компактном виде:
λx = (φi+1,j — 2 φi,j + φi-1,j)/hx2;
λy = (φi,j+1 — 2 φi,j + φi,j+1)/hy2. (3.7)
При переходе от дифференциальной краевой задачи к разностной необходимо также аппроксимировать граничные условия. Совокупность разностного уравнения и разностных краевых условий называют разностной схемой краевой задачи.
Кажущаяся простота построения разностной схемы часто бывает обманчива. В реальных задачах при построении разностных схем могут возникнуть существенные проблемы. Главная из них – это построение сходящейся разностной схемы. Понятие сходимости разностной схемы тесно связано также с понятием точности и устойчивости.
Большинство задач, описываемых ОДУ, можно решить также с помощью математических пакетов, например, MathCAD-2000, который имеет ряд встроенных функций для численного решения различных дифференциальных уравнений /12/:
- решение обыкновенных дифференциальных уравнений (odesolve, rkfixed);
- решение гладких систем (Bulstoer);
- решение жестких систем (Stiffb, Stiffr);
- решение медленно изменяющихся систем (Rkadapt);
- нахождение последней точки на интегрируемом интервале (bulstoer, rkadapt, stiffb, stiffr );
- решение краевых задач с двумя ограничениями (bvalfit, sbval);
- решение дифференциальных уравнений в частных производных (relax, multigrid).
Несмотря на различные методы поиска решения, каждая из них требует задания следующих величин – начальных условий и набора точек, в которых нужно найти решение, а также дифференциального уравнения, записанного в определенном формате.
Каждая функция возвращает матрицу, содержащую значения аргумента, функции и ее младших производных.
Приведем несколько примеров, иллюстрирующих применение встроенных функций MathCAD для решения ОДУ и ДУЧП.
Пример 1. Пусть дано дифференциальное уравнение второго порядка:
![]()
Известно, что решением данного дифференциального уравнения является полином Чебышева первого порядка с n степенями свободы. Его точное решение можно получить с помощью встроенной в MathCAD функции Tcheb(n,x).
Построим разностную схему этого дифференциального уравнения
![]()
и разрешим его относительно yi+1:
![]() .
.
В среде MathCAD будем иметь:
![]()


Рис. 3.3. Графики функций y и k(), полученных при решении ОДУ
При решении краевых задач с граничными условиями часто выполняют преобразования граничных условий к начальным. Такое преобразование дает возможность функции группы rkfixed() использовать для решения некоторых дифференциальных уравнений с частными производными (ДУЧП).
Функция bvalfit() выполняет преобразования граничных условий, заданных на интервале поиска решения и возвращает вектор начальных условий в неизвестной точке х1. Она имеет формат:
bvalfit(v1,v2,x1,x2,xf,D,load1,load2,score),
где: v1 – вектор, содержащий неполные граничные условия для х1; v2 – вектор, содержащий неполные граничные условия для х2; х1 и х2 – начальные и конечные точки интервала, на котором решается ДУЧП; xf – точка на интервале (х1,х2), в которой искомая функция при поиске решения от х1 и х2 имеет одинаковые значения; D – n-мерный вектор младших производных; load1 – искомый вектор граничных значений для точки х1; load2 – искомый вектор граничных значений для точки х2; score – n-мерный вектор значений функции и ее производных в точке xf. Если score(xf,y)=y, то все значения производных справа и слева совпадают.
Пример 2. Решить уравнение:
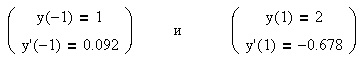 |
Преобразуем граничные условия в начальные (xf – точка разрыва):
Таким образом, в результате преобразования граничных условий получим:
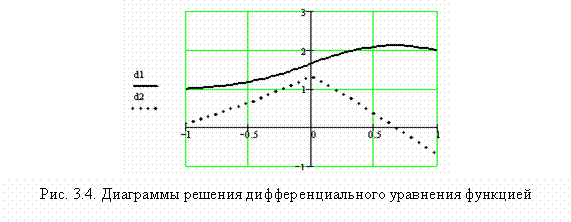 |
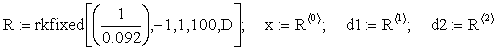
Функция sbval() вычисляет недостающие начальные условия в точке х1и тем самым преобразует краевую задачу в задачу Коши. Она имеет формат
sbval(v,x1,x2,D,load,score),
где: v – вектор для начальных значений младших производных (задаются как начальные приближения для искомых производных в точке х1); х1, х2 – начальное и конечное значение интервала поиска решения; D – n-мерный вектор младших производных; load – вектор начальных условий для точки х; score – разность производных и их граничных значений в точке х2.
 |
Пример 3. Решить дифференциальное уравнение с граничными значениями:
После нахождения искомых начальных условий можно задачу решать с помощью функций группы rkfixed().
Для решения дифференциального уравнения в частных производных типа уравнения Пуассона используется функция relax(a, b, c, d, e, f, u, rjac), возвращающая квадратную матрицу, в которой:
- расположение элементов матрицы соответствует расположению сетки внутри квадратной области;
- значение элемента матрицы аппроксимирует значение искомого решения.
Для обеспечения сходимости решения используется релакционный метод. Эту функцию целесообразно использовать, если граничные значения на концах области отличны от нуля. Если все граничные значения на концах области равны нулю, то необходимо использовать функцию multigrid(). Пример использования функции relax() (рис. 3.5):

Рис. 3.5. Диаграммы решения ДУЧП функцией relax()