Так как процентные деньги по схеме сложных процентов не выплачиваются сразу по мере их начисления, а присоединяются к первоначальной сумме долга, то долг, таким образом, увеличивается на невыплаченную сумму процентов, и последующее начисление процентов происходит на увеличенную сумму долга. Таким образом, наращенная сумма долга по схеме сложных процентов определяется:
· за один период начисления по формуле (2.2)
FV = PV + I = PV + PV · i = PV (1 + i);
· за два периода начисления по следующей формуле
FV = (PV + I) (1 + i) = PV (1 + i) (1 + i) = PV (1 + i)2.
Следовательно, формула для определения наращенной суммы долга по схеме сложных процентов за n периодов начисления имеет следующий вид:
FV = PV (1 + i)n = PV · kн, (3.1)
где FV – наращенная сумма долга; PV – первоначальная сумма долга; i – ставка процентов в периоде начисления; n – количество периодов начисления; kн – коэффициент (множитель) наращения сложных процентов.
Различие начисления простых и сложных процентов состоит в базе их начисления. Если простые проценты начисляются все время на одну и ту же первоначальную сумму долга, т.е. база начисления является постоянной величиной, то сложные проценты начисляются на увеличивающуюся с каждым периодом начисления базу.
 |
Коэффициенты (множители) наращения, зависящие от процентной ставки и числа периодов наращения, табулированы. При пользовании финансовыми таблицами необходимо следить за соответствием длины периода и процентной ставки. Экономический смысл множителя наращения состоит в том, что он показывает, чему будет равна одна денежная единица (один рубль, один доллар и т.п.) через n периодов при заданной процентной ставке (i).
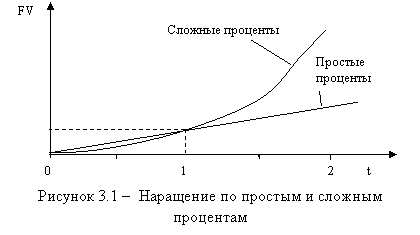
Графическая иллюстрация соотношения наращенной суммы по простым и сложным процентам представлена на рисунке 3.1. Как видно из рисунка, при краткосрочных ссудах начисление по простым процентам предпочтительнее, чем по сложным процентам; при сроке в один год разница отсутствует, но при среднесрочных и долгосрочных ссудах наращенная сумма, рассчитанная по сложным процентам, значительно выше, чем по простым. То есть, при любом i,
|
если 0 < n < 1, |
то (1 + ni) > (1 + i)n ; |
|
если n > 1, |
то (1 + ni) < (1 + i)n ; |
|
если n = 1, |
то (1 + ni) = (1 + i)n . |
Таким образом, для лиц, предоставляющих кредит:
· более выгодна схема простых процентов, если срок ссуды менее года (проценты начисляются однократно в конце года);
· более выгодной является схема сложных процентов, если срок ссуды превышает один год;
· обе схемы дают одинаковый результат при продолжительности периода один год и однократном начислении процентов.