В некоторых ситуациях описание связи между переменными в виде линейных соотношений допустимо, а в некоторых – нет. Хотя трудно сформулировать  общее правило применения линейных моделей, можно все же дать следующую рекомендацию по использованию моделей. В повседневных повторяющихся тактических операциях, когда имеется уже опыт в принятии решений и поэтому диапазон возможного выбора невелик, допустимо использование линейных моделей. В крупномасштабных новых стратегических операциях, когда нет ясного представления о характере оптимального решения, необходимы нелинейные модели.

Как известно из курса математического анализа, если мы рассматриваем задачу поиска экстремума  функции многих переменных без каких-либо ограничений на значения переменных , то в предположении непрерывной дифференцируемости функции  для нахождения ее экстремума достаточно приравнять к нулю все ее частные производные, найти решения системы уравнений

                    (3.1)

и выбрать из них те, которые доставляют функции соответствующий экстремум (максимум или минимум).

Однако если на значения переменных наложены ограничения, то задача усложняется. Так, если мы ищем экстремум функции одной переменной на отрезке, то надо отдельно проверять концы отрезка, так как в них может быть экстремум и не при нулевом значении производной. Если же имеется функция многих переменных и граница области изменения переменных имеет достаточно сложный вид, то проверить все ее точки не представляется возможным. Кроме того, система уравнений (3.1) при большом числе переменных может иметь слишком много решений, найти которые и выбрать среди них нужные точки экстремума также практически очень сложно.

Подчеркнем здесь, что нас интересует глобальный (абсолютный) экстремум функции, а у нее может существовать множество локальных экстремумов.

В классическом анализе рассматривается случай наличия ограничений на переменные в экстремальной задаче, а именно, ограничений типа равенств:

                  (3.2)

В этом случае используется известный метод множителей Лагранжа, который состоит в построении функции Лагранжа

                (3.3)

где  – вектор множителей Лагранжа, и нахождения решений системы уравнений:

                 (3.4)

Система (3.4) состоит из (n + m) уравнений с (n + m) неизвестными  . При некоторых (вообще говоря, достаточно жестких) предположениях точки

экстремума функции на множестве, заданном ограничениями(3.2), и соответствующие им множители Лагранжа находятся среди решений системы (3.4).

Экстремальные задачи при ограничениях типа неравенств в классическом анализе не рассматриваются. В этом случае возникают дополнительные трудности, для преодоления которых метод множителей Лагранжа нуждается в обобщении. Такие вопросы рассматриваются в математическом программировании, к ним мы сейчас и переходим.

Общей задачей математического программирования называется задача отыскания верхней грани функции при ограничениях

              (3.5)

                                    (3.6)

где R – некоторое непустое подмножество n-мерного евклидова пространства .

Если ввести множество

                  (3.7)

то кратко эту задачу можно записать как задачу определения величины:

                          (3.8)

Напомним, что верхней гранью функции называется наименьшее из чисел, ограничивающих функцию сверху. Отличие этого понятия от понятия максимума функции заключается только в том, что для максимума подразумевается существование точки, в которой функция принимает максимальное значение, а для верхней грани это не обязательно, т.е. верхняя грань может не достигаться. Отсутствие точек максимума связано или с разрывностью функции, или с незамкнутостью множества, на котором она задана, или с его неограниченностью (рис. 3.1 и рис. 3.2).

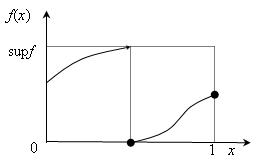
Рис. 3.1. Пример верхней грани функции

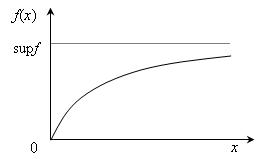
Рис. 3.2. Графическое представление верхней грани функции

Далее удобно будет использовать понятие верхней грани, так как некоторые множества будут заведомо неограничены, но читатель может для простоты подразумевать под верхней гранью максимум и заменять символ «sup» на «max» (аналогично для нижней грани «inf» и минимума «min»).

Так как ограничение типа равенства (3.2) можно заменить двумя ограничениями типа неравенства  , а ограничение вида  можно заменить на ограничение вида , то система ограничений (3.5) действительно имеет общий вид.

Разделение ограничений на ограничения (3.5), (3.6) не носит принципиального характера, так как каждое из них может быть записано в одном из этих двух видов, но иногда оказывается полезным. Так, в задаче линейного программирования мы записывали отдельно условие неотрицательности (), хотя это частный вид линейного ограничения. Кстати, нетрудно видеть, что задача линейного программирования – это частный случай задачи (3.8). Действительно, если  и  – линейные функции, R – неотрицательный ортант и систему ограничений (3.5) переписать в виде обратных неравенств, то получим задачу линейного программирования в стандартной форме.

Если верхняя грань в задаче (3.8) достигается, то обычно ставится задача нахождения помимо величины  и точки реализации верхней грани в (3.8) , для которой:

.

Точку  называют решением, или точкой глобального максимума, или оптимальным планом, множество Х – допустимым множеством или множеством допустимых планов (вообще говоря, оно может быть и пустым), его точки – допустимыми точками или допустимыми планами.

Для задачи (3.8) функция вида (3.3) также является функцией Лагранжа, а у – вектором множителей Лагранжа. Однако в общем случае метод множителей Лагранжа в обычном виде для ее решения не применим.