Для изображения лежащих в трехмерном пространстве объектов координаты точек (мировые координаты) преобразуются сначала в координаты в пространстве изображения, а затем – в экранные.

Для произвольных трехмерных векторов a, b и c через (a,b,c) обозначим смешанное произведение. Скалярное произведение векторов будем обозначать через a×b, векторное – через a´b. Пусть наблюдатель находится в точке (x_V,y_V,z_V). Центральной проекцией произвольной точки (x,y,z) называется точка пересечения плоскости проекции и луча, соединяющего точку (x_V,y_V,z_V) наблюдения с точкой (x,y,z). Параллельная проекция получается из центральной, если точку наблюдения бесконечно удалить в некотором направлении.

Рассмотрим, например, шар в трехмерном пространстве. Соединяя точку наблюдения (x_V,y_V,z_V) с каждой точкой шара, мы получим круговой конус. Так как пересечение произвольной плоскости с конусом является эллипсом, то центральной проекцией шара будет эллипс, превращающийся в круг только в тех случаях, когда плоскость проекции перпендикулярна прямой, проходящей через точку наблюдения и центр шара.

Опишем формулы преобразования координат при параллельной и центральной проекции.

Параллельная проекция. Пусть задана декартова система координат (x,y,z). Рассмотрим произвольную плоскость P, проходящую через некоторую точку (x₀,y₀,z₀), радиус-вектор которой равен r₀, параллельно векторам u₁ и u₂ (рис. 16) /15/.

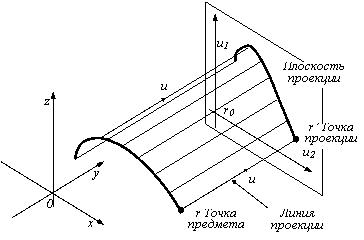
Рис. 16. Плоская параллельная проекция

Пусть u – произвольный вектор. Тогда для каждой точки r трехмерного пространства существует единственная тройка (x’,y’,z’) вещественных чисел такая, что r=r₀+x’u₁+y’u₂+z’u.

Пару чисел (x’,y’) мы будем называть координатами параллельной проекции точки (x,y,z) на плоскость P вдоль направления u, или параллельной проекцией на плоскость P параллельно вектору u (рис. 17) /15/.

Чтобы найти x’, y’ и z’, умножим обе части равенства

 r-r₀=x’u₁+y’u₂+z’u скалярно на векторы, выбранные таким образом, что в правой части остается лишь один ненулевой член. Умножая на u₁´u, приходим к равенству (r-r₀,u₁,u)=y'(u₂,u₁,u). Умножая на u₂´u, получим

(r-r₀,u₂,u)=x‘(u₁,u₂,u).

Наконец, скалярное произведение на u₁´u₂ приводит к равенству

(r–r₀,u₁,u₂)=z'(u,u₁,u₂).

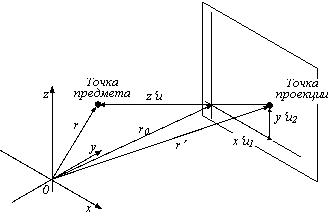Рис. 17. Параллельная проекция

Отсюда вытекает, что координаты (x’,y’) проекции вдоль направления u на плоскость П можно вычислить с помощью формул

x’=(r-r₀,u₂,u)/(u₁,u₂,u),

y’=-(r-r₀,u₁,u)/(u₁,u₂,u).

При применении алгоритмов удаления невидимых линий необходимо знать координату, характеризующую степень удаленности точки от плоскости P. Согласно выкладкам, эта координата равна  z’=(r-r₀,u₁,u₂)/(u₁,u₂,u).

Пример 3.1. Рассмотрим параллельную проекцию трехмерного пространства на плоскость Oyz в направлении вектора u=(1,0.7,0.7). Плоскость Oyz можно задать векторами u₁=(0,1,0), u₂=(0,0,1).

Смешанное произведение (u₁,u₂,u) равно 1. Поэтому

,                       ,

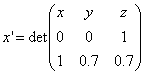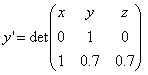отсюда находим x’=-0.7x+y, y’=-0.7x+z.

Пример 3.2. Рассмотрим ортогональную проекцию на плоскость, проходящую через начало координат, заданную единичным вектором нормали n. В этом случае u=n. Вектор u₁, обычно, (например, в архитектуре или в военном деле) берут лежащим в горизонтальной плоскости Oxy. Этот вектор должен быть ортогонален вектору u, поэтому при u₁={x,h,0} выполнено соотношение xu_x+hu_y=0. Решая это уравнение получаем u₁, а затем u₂:

u₁={-u_y/sqrt(u_x²+ u_y²),u_x/sqrt(u_x²+u_y²),0},

u₂={-u_xu_z,-u_yu_z,u_x²+u_y²}/sqrt(u_x²+u_y²).

Центральная проекция. Пусть задана плоскость с началом координат r₀ и базисными векторами u₁ и u₂ (рис. 18) /15/. Требуется изобразить на плоскости проекцию точки r=(x,y,z) из точки наблюдения r_V. Пусть (x’,y’) – искомые координаты. Тогда для некоторого lIR выполнено равенство r₀+x’u₁+y’u₂=r_V+l(r-r_V).

Координаты x’, y’ будут вычисляться по формулам

x’=(r_V-r₀,u₂,r-r_V)/(u₁,u₂,r-r_V),

y’= — (r_V -r₀,u₁,r-r_V)/(u₁,u₂,r-r_V).

Число l характеризует дальность точки r, в частности при l<1 точка r лежит перед плоскостью, а при l>1 – за плоскостью проекции,

l=-(r_V -r₀,u₁,u₂)/(u₁,u₂,r-r_V )

(ближе всех лежат точки, для которых l=0).

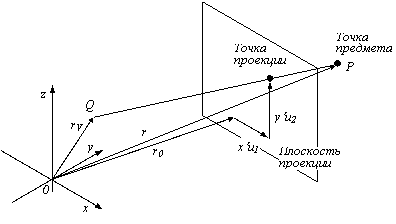Рис. 18. Центральная проекция

Если (u₁,u₂,r_V-r₀)>0, то в качестве третьей координаты z’, чтобы система координат (x’,y’,z’) была правой, берется значение z’=-l. Поскольку l>0, для всех лежащих в поле зрения наблюдателя точек r, то координата z’ будет меньше нуля.

Укажем теперь, как можно получить центральную проекцию из параллельной. Пусть u – произвольный вектор, коллинеарный вектору r_V-r₀. Тогда существует число d такое, что r_V–r₀=du. Рассмотрим проекцию, параллельную вектору u, на плоскость, заданную векторами r₀,u₁ и u₂. Предположим, что координаты параллельной проекции точки (x,y,z) вдоль вектора u равны (x»,y»,z»). Тогда

x»=(r-r₀,u₂,u)/(u₁,u₂,u),

y«=-(r-r₀,u₁,u)/(u₁,u₂,u),

z«=(r-r₀,u₁,u₂)/(u₁,u₂,u).

Подставляя приведенные выше для центральной проекции формулы, убеждаемся в том, что координаты центральной проекции будут вычисляться по следующим формулам:

x’=x»d/(d-z»), y’=y»d/(d-z»), z’=-l=d/(d-z»),

справедливость которых легко проверить аналогично, исходя из геометрических соображений.

При применении алгоритмов удаления невидимых линий полагают, что ось z’ перпендикулярна плоскости (x’,y’), а числа x’ и y’ служат координатами проекции.

Обычно вектор r₀ выбирают так, чтобы прямая, соединяющая точку r_V с точкой r₀, была перпендикулярна плоскости проекции (рис. 19) /15/. В этом случае r_V-r₀=du, где u=u₁´u₂, а d – расстояние от точки r_V до плоскости, поэтому

x’=-d(r-r₀)×u₁/((r-r₀)×u-d);

y’=-d(r-r₀) ×u₂/((r-r₀) ×u-d);

z‘=-l=d/((r-r₀) ×u-d).

Пример 3.3. Пусть ось Oz параллельна плоскости проекции. Положим u₂=(0,0,1). Рассмотрим единичный вектор u₁, перпендикулярный вектору u₂, лежащий в плоскости проекции. Положим u=u₁´u₂. Выберем так вектор r₀, чтобы вектор r₀-r_V был перпендикулярен плоскости проекции. Тогда r₀=r_V-d(u₁´u₂), где d – расстояние от точки наблюдения до плоскости проекции. Вектор u лежит в плоскости Oxy, поэтому существует некоторый угол a такой, что u=(cosa,sina,0). Выберем третьим вектор u₁=(-sina,cosa,0), этот вектор перпендикулярен векторам u₂ и u, и имеет единичную длину.

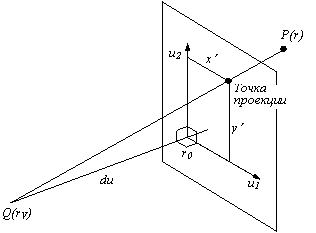
Рис. 19. Центральная проекция

Если предположить, что координаты точки наблюдения равны (x_V,y_V,z_V), то координаты центральной проекции точки (x,y,z) будут вычисляться по формулам

x’=-d((x-x_V)(-sina)+(y-y_V)cosa)/((x-x_V)cosa+(y-y_V)sina);

y’=-d(z-z_V)/((x-x_V)cosa+(y-y_V)sina);

z’=-l=d/((x-x_V)cosa+(y-y_V)sina).