Одним из ключевых решений относительно объема производства является решение, определяющее критический объем производства. Как известно, речь идет об установлении такой величины объема производства, когда совокупные затраты предприятия равны его выручке.
Концепция сумм покрытия исходит из того условия, что в краткосрочном периоде выручка должна покрывать все переменные затраты. При этом превышение выручки над всеми перенесенными затратами принято называть /12, 17, 24, 41/ суммой покрытия. Таким образом, для расчета суммы покрытия может быть использована следующая формула:
DB = TR – TVC = П + TFC,
где DB – сумма покрытия; TR – выручка от реализации; TVC – совокупные переменные затраты, связанные с ценным объемом продаж; П – прибыль от реализации; TFC – совокупные постоянные затраты.
С учетом этого можно найти критический объема производства:
DB = TFC. (3.1)
Из выражения (3.1) следует, что предприятие достигает точки безубыточности в том случае, когда выручка покрывает не только переменные, но и все постоянные затраты.
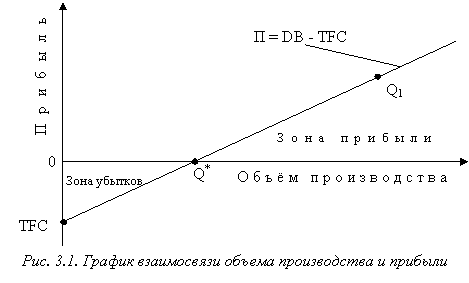
В 30-е годы ХХ века В. Рауменштраух, Дж. Ульямс, Ч. Кноппель разработали график критического объема производства. Один из вариантов этого графика показан на рисунке 3.1. Следует особо обратить внимание на то, что при построении графика критического объема производства делается ряд допущений /28, 40/:
1) цены на реализуемые товары и потребляемые производственные ресурсы остаются неизменными;
2) переменные затраты и выручка имеют линейную зависимость от уровня производства;
3) затраты предприятия можно однозначно разделить на постоянные и переменные;
4) ассортимент реализуемых товаров остается постоянным;
5) объем продаж и объем производства равны.
Для построения графика (рис. 3.1) рекомендуется /16/ придерживаться следующей последовательности действий;
1) на оси ординат откладывают значение постоянных затрат (точка TFC) при условии, что объем производства равен нулю;
2) рассчитывают ожидаемую сумму прибыли при заданном значении объема производства. Соответствующая точка наносится на координатную плоскость (например, точка Q1);
3) по двум точкам строится прямая, характеризующая динамику прибыли;
4) точка пересечения прямой с осью абсцисс позволяет установить критический объем производства.
Из рис. 3.1 видно, что после прохождения точки Q*, соответствующей критическому объему производства, все вклады в покрытие становятся прибылью.
Аналитически критический объем производства можно определить следующим образом:
Q* = ![]() =
= ![]() ,
,
где Р – цена единица товара; VC – удельные переменные затраты; DBу – сумма покрытия в расчете на единицу товара; Q* – критический объем производства в натуральном выражении.
Для того чтобы рассчитать критический объем производства в стоимостном выражении, можно использовать формулу:
TR* = ![]() .
.
Для определения критического объема, которого нужно достичь при условии снижения цены и сохранения прежней суммы покрытия, рекомендуется /28/ воспользоваться соотношением:
Q1* = ![]() ,
,
где Q0*, Q1* – критический объем производства соответственно до и после снижения цен; ![]() ,
, ![]() – удельная сумма покрытия соответственно до и после снижения цен.
– удельная сумма покрытия соответственно до и после снижения цен.
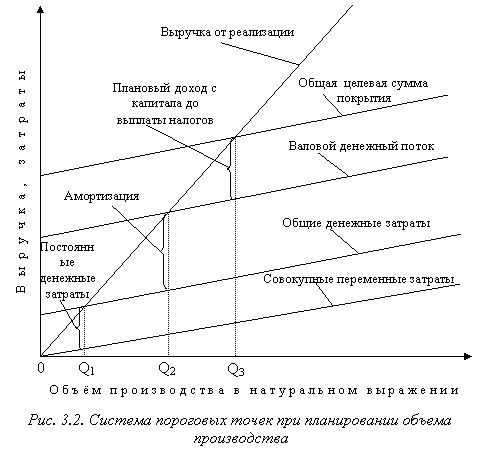
Полученный в результате расчета критического объема результат можно уточнить, если проанализировать структуру покрытия совокупных постоянных затрат. При этом в процессе анализа можно выделить такие группы, как постоянные денежные затраты, амортизация, плановый доход с капитала до выплаты налогов. В конечном счете, формируется система пороговых точек (рис. 3.2), позволяющих формировать определенные цели развития предприятия.
Объем Q1 (см. рис. 3.2) соответствует точке финансовой безубыточности, при достижении которой обеспечивается покрытие постоянных денежных затрат. С учетом этого объем Q1 может выступать в качестве сигнала о возможных финансовых проблемах.
В свою очередь, объем Q2 представляет собой точку безубыточности, при достижении которой обеспечивается простое воспроизводство. В данном случае амортизация формирует целевую сумму покрытия, необходимую для финансирования новых инвестиций за счет амортизации.
Наконец, объем Q3 – это целевая точка безубыточности по бюджету. С ее помощью устанавливается величина реинвестируемой прибыли, которая способна обеспечить развитие предприятия.
Как уже отмечалось, определение критического объема производства на основе подхода с использованием сумм покрытия связано с необходимостью выполнения ряда
допущений. Однако в действительности это зачастую оказывается весьма трудно достижимым делом.
Рассмотрим случай, когда в отношении объема продаж существует неопределенность, и он подчиняется нормальному закону распределения. В таком случае Дж. К. Сим и Дж. Г. Сигел рекомендуют использовать типовой статический метод, позволяющий определить суммарное воздействие неопределенности объема продаж на сумму покрытия:
DBож = DBу · М (Q) = (Р – VC) · М (Q),
где DBож – ожидаемая сумма покрытия в условиях неопределенности; М(Q) – математическое ожидание объема продаж.
С учетом этого ожидаемая прибыль составляет:
Пож = DBож – TFC = (Р – VC) · М (Q) – TFC.
Вследствие неопределенности объема продаж прибыль также является случайной величиной, для характеристики которой вычисляется среднее квадратическое отклонение:
σп = (Р – VC) σQ,
где σп, σQ – среднее квадратическое отклонение соответственно прибыли и объема продаж.
Для оценки вероятности непревышения точки безубыточности определяется параметр Z:
Z = ![]() .
.
Рассчитанный таким образом параметр Z позволяет установить число среднеквадратичных отклонений от точки безубыточности в сторону ожидаемой величины при
были. Используя параметр Z, по таблицам нормального распределения можно определить искомую вероятность убыточной деятельности.