Устойчивость замкнутой линейной системы зависит от расположения корней характеристического уравнения на комплексной плоскости р. Условие устойчивости заключается в том, что все корни должны находиться в левой полуплоскости. Так как дискретные системы с АИМ и  являются линейными, указанное условие распространяется и на них.

Каждому корню  на плоскости р согласно выражению (2.3) соответствует корень  на плоскости z. Очевидно, что любой из р-корней, лежащий на мнимой оси, определяет z-корень, для которого  и который, следовательно, расположен на единичной окружности, проведенной из начала координат комплексной плоскости z.

Всем корням  с отрицательными вещественными частями соответствуют z-корни, у которых . Если же вещественная часть корня  положительна, то . Таким образом, замкнутая линейная дискретная система устойчива, если все z-корни ее характеристического уравнения лежат внутри круга единичного радиуса с центром в начале координат.

Пример 18

Необходимо оценить устойчивость замкнутой дискретной системы, структурная схема которой приведена на рис. 3.1. Передаточные функции в непрерывной части системы равны:

;             .

Интервал квантования равен:  Передаточная функция замкнутой системы:

.

Полюса полученной передаточной функции (корни характеристического уравнения) . Модуль комплексно-сопряженных корней равен:

.

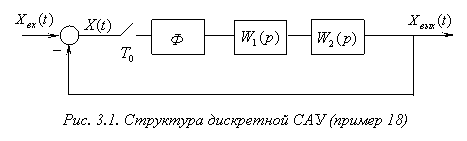Так как все три корня находятся внутри единичного круга, можно сделать заключение, что система устойчива.

Для дискретных систем, порядок характеристического уравнения которых превышает третий, определение корней этих уравнений представляет собой достаточно трудную задачу. Это обусловливает широкое применение косвенных методов оценки устойчивости (критериев устойчивости), не предполагающих вычисление корней характеристического уравнения.