Задача 1

Построить LU-разложение матрицы А. Вычислить значение определителя матрицы А методом Гаусса:

А=.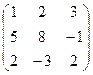

Решение

Умножим  первую строку на -5 и прибавим ко второй. Умножим первую строку на  –2 и прибавим к третьей. Получим:

Умножим вторую строку на –7/2 и прибавим к третьей. Получим матрицу:

U = 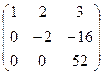     и          матрицу L = .

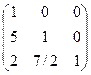Определитель матрицы А находим по формуле: ,    det A = -104.

Задача 2

Решить систему линейных уравнений методом Гаусса с частичным выбором ведущего элемента (по столбцу):

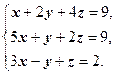
Решение

Прямой ход метода Гаусса

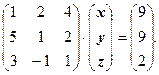
Прежде всего, выбираем максимальный по модулю элемент в первом непреобразованном столбце:

,      , следовательно,  ведущим элементом является 5.

Ведущим элементом является элемент , поэтому необходима перестановка строк 1 и 2:

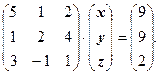
Умножим первое уравнение на –1/5 и прибавим ко второму. Умножим первое уравнение на –3/5 и прибавим к третьему. Получим:

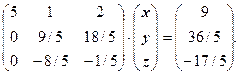
Рассмотрим следующий непреобразованный столбец:

,        , следовательно, ведущим элементом является 9/5, перестановка строк не требуется. Умножим второе уравнение на 8/9 и прибавим к третьему. Получим:

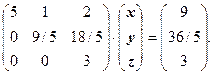
Мы получили систему линейных уравнений с верхней треугольной матрицей. Прямой ход метода Гаусса с частичным выбором ведущего элемента закончен.

Обратная подстановка

3z = 3,   z = 1,

,           y = 2,

5x + y + 2z = 9,             x = 1.

Задача 3

Решить систему линейных уравнений методом Гаусса-Жордана с частичным выбором ведущего элемента:

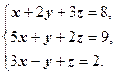
Решение

Прямой ход

В методе Гаусса-Жордана первый шаг прямого ходя совпадает с первым шагом прямого хода метода Гаусса. Найдём максимальный по модулю элемент первого столбца (это элемент а₂₁), поменяем местами первое и второе уравнения, получим:

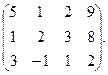
Умножим первое уравнение на –1/5 и прибавим ко второму, умножим первое уравнение на –3/5 и прибавим к третьему, получим:

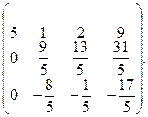
На втором шаге непреобразованный столбец состоит из двух элементов: 9/5, -8/5. Максимальный по модулю элемент  расположен на главной диагонали, следовательно, не нужно менять местами уравнения. Чтобы занулить  элементы а₃₂ и а₁₂ , умножим второе уравнение на 8/9 и прибавляем к третьему, умножаем второе уравнение на –5/9 и прибавим к первому, получим:

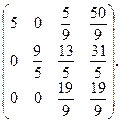
На третьем шаге зануляем элементы а₁₃ и а₂₃ с помощью третьего уравнения. Для этого умножим третье уравнение на  -117/95 и прибавим ко второму, умножим третье уравнение на  -5/19 и прибавим к первому, получим:

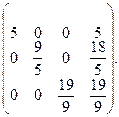
Мы получили систему линейных уравнений с диагональной матрицей. На этом прямой ход метода Гаусса – Жордана закончен.

Обратная подстановка

В данном случае обратная подстановка заключается в решении системы линейных уравнений с диагональной матрицей:

Ответ:  x = 1,  y = 2,  z = 1.

Задача 4

Построить и обосновать алгоритм решения системы линейных уравнений методом итераций с точностью ε:

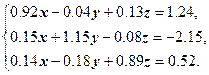
Оценить число шагов k, необходимых для достижения точности ε.

Решение

1. Необходимо обосновать, что определитель матрицы не равен нулю:

  

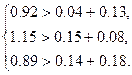
Следовательно, матрица А является матрицей с диагональным преобладанием, значит, det A ≠ 0.

2. В нашем случае можно считать:  ,  где  – единичная матрица, тогда D = b.

Найдем С и докажем, что :

                      

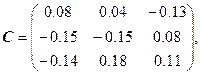
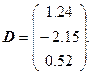
Вычислим первую норму С:

.

Следовательно, метод итераций сходится для любого x₀, выбираем вектор начального приближения:   .

3. Формула метода:   .

4. Условие остановки итерационного процесса:

,   .

5. Оценка числа шагов k, необходимых для достижения точности ε:

,   ,   .

.

При выполнении этого условия х^(k) является приближенным решением системы линейных уравнений с точностью e, полученным методом итераций.