Определение 3.2.1.  Недетерминированным МП-автоматом называется семерка   M = <A, Q, Г, , q₀, z₀, F>,

где       А — конечное множество входных символов (входной алфавит);

            Q — конечное множество внутренних состояний (алфавит состояний);

            Г — конечное множество магазинных символов;

            q₀Q — начальное состояние автомата;

            z₀Г — начальный (первый) символ в магазинной памяти;

            FQ — множество заключительных состояний;

             — отображение QxAxГ в множество подмножеств QxГ*, т.е. отображение вида : QxAxГ (QxГ*).

Схема МП-автомата показана на рис. 3.4. Автомат имеет конечное множе­ство состояний, конечное множество входных символов и неограниченную снизу вспомогательную ленту (называемую лентой магазинной памяти или магазинной памятью). «Дно» магазина (самый нижний символ) отмечается специальным символом, называемым маркером дна. Пусть это будет символ #. Магазинная память определяется свойством «первым введен — последним выведен». При записи символа в магазин, его содержимое сдвигается на одну ячейку «вниз», а на освободившееся место записывается требуемый символ. В этом случае говорят, что символ «вталкивается» в магазин.

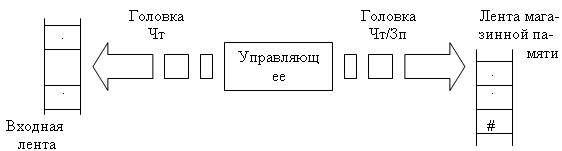
Рис. 3.4. Схема автомата с магазинной памятью

Для чтения доступен только самый последний (т.е. верхний) символ магази­на. Этот символ после чтения может либо остаться в магазине, либо быть уда­лен из него, т.е. «вытолкнут» из магазина. За один такт работы МП-автомата из магазина можно удалять не более одного символа.

Каждый шаг работы МП-автомата задается множеством правил перехода ав­томата из одних состояний в другие. Переходы в общем случае определяются:

· состоянием МП-автомата;

· верхним символом магазина;

· текущим входным символом.

Множество правил перехода называется управляющим устройством. В за­висимости от получаемой информации, управляющее устройство реализует один такт работы МП-автомата, который включает в себя три операции (в скоб­ках указано обозначение операций):

1) операции над магазином:

· втолкнуть в магазин определенный символ (ВТОЛКНУТЬ (А), где А — магазинный символ);

· вытолкнуть верхний символ из магазина (ВЫТОЛКНУТЬ);

· оставить содержимое магазина без изменений;

2) операции над состоянием:

· перейти в заданное новое состояние (СОСТОЯНИЕ (S), где S — следующее состояние;

· остаться в прежнем состоянии;

3) операции над входом:

· перейти к следующему входному символу и сделать его текущим (СДВИГ);

· оставить данный входной символ текущим, т.е. держать его до следующего шага (ДЕРЖАТЬ).

Обработку входной цепочки МП-автомат начинает в некотором выделен­ном состоянии при определенном содержимом магазина. Затем автомат вы­полняет операции, задаваемые его управляющим устройством. При этом выполняется либо завершение обработки, либо переход в новое состояние. Если выполняется переход, то он дает новый верхний символ магазина, новый теку­щий символ, автомат переходит в новое состояние и цикл работы автомата повторяется.

МП-автомат называется МП-распознавателем, если у него два выхода ДОПУСТИТЬ и ОТВЕРГНУТЬ.

Рассмотрим МП-автомат [14], распознающий слова языка L = {0ⁿlⁿ | n1}, т.е. слова, состоящие из n нулей, вслед за которыми идет ровно такое же коли­чество единиц. Для этого автомата А = {0, 1, }, Q = {q₁, q₂}, Г = {z, #},  — символ конца цепочки на входной ленте, # — маркер дна магазина, q₁ — на­чальное состояние, # — начальное содержимое магазина. Работа управляюще­го устройства для данного автомата (а это МП-распознаватель) осуществляется в соответствии с управляющими

таблицами, изображенными на рис. 3.5, а и б для состояний q₁, и q₂ соответственно. В таблицах показаны действия автомата для каждого сочетания входного символа и верхнего символа магазина.

Работа МП-автомата при распознавании конкретной цепочки описывается обычно в виде последовательности конфигураций МП-автомата. При линей­ном представлении конфигураций слева изображается магазин, в середине — состояние, справа — необработанная часть входной цепочки. Ниже показана такая последовательность конфигураций при анализе МП-автоматом входного слова 000111:

МАГАЗИН	СОСТОЯНИЕ	ВХОДНАЯ ЛЕНТА
#	q­1	000111
#z	q­1	00111
#zz	q­1	0111
#zzz	q­1	111
#zz	q­2	11
#z	q­2	1
#	q­2
ДОПУСТИТЬ

а)

Состояние q₁

Магазин	Вход
	0	1
Z	СОСТОЯНИЕ (q1) ВТОЛКНУТЬ (z) СДВИГ	СОСТОЯНИЕ (q2) ВЫТОЛКНУТЬ СДВИГ	ОТВЕРГНУТЬ
#	СОСТОЯНИЕ (q1) ВТОЛКНУТЬ (z) СДВИГ	ОТВЕРГНУТЬ	ОТВЕРГНУТЬ

б)

Состояние q₂

Магазин	Вход
	0	1
Z	ОТВЕРГНУТЬ	СОСТОЯНИЕ (q2) ВЫТОЛКНУТЬ СДВИГ	ОТВЕРГНУТЬ
#	ОТВЕРГНУТЬ	ОТВЕРГНУТЬ	ДОПУСТИТЬ

Рис. 3.5. Управляющая таблица для состояния q₁ (а)  и  q₂ (б) МП-распознавателя языка L = {0ⁿlⁿ | n1}

Другой способ описания (более формальный) МП-автомата — в виде команд. Команда записывается в виде:

(q, a, z)  {(q₁, ₁), …, (q_m, _m)},

где q, q₁, …, q_m Q; aA; zГ; ₁,₂, …, _m Г*.

Интерпретируется следующим образом: МП-автомат находится в состоя­нии q, считывает входной символ а и верхний символ магазина z, переходит в состояние q_i, заменяя в магазине символ z на символ _i, lim и продвигает входную головку на один символ.

Если же при выполнении команды сдвига входной ленты не выполняется, то команда записывается в виде:

(q, , z)  {(q₁, ₁), …, (q_m, _m)},

и используется лишь для изменения магазина.

Различают детерминированные и недетерминированные МП-автоматы. Если среди команд МП-автомата нет двух таких, у которых совпадают части, стоящие слева от стрелки, и не совпадают части, стоящие справа от стрелки, то МП-авто­мат называют детерминированным. В противном случае, т.е. когда для текущих входном и магазинном символов и заданно­го состояния, возможны переходы автомата в различные состояния, его называют недетерминированным.