При решении некоторых прикладных задач нередко возникает необходимость найти маршрут, соединяющий заданные вершины в графе G. Данная задача решается при использовании алгоритма Тэрри.
Рассмотрим более сложную задачу: нахождение пути (маршрута) с минимальным числом дуг (ребер).
Определение. Путь в орграфе D из вершины v в вершину w, где v 
w, называется кратчайшим, если он имеет минимальную длину среди всех путей орграфа D из v и w. Аналогично определяется и кратчайший маршрут в графе G.
Утверждение. Любой кратчайший путь (маршрут) является простой цепью.
Рассмотрим задачу поиска минимального пути (маршрута). Введем некоторые обозначения. Пусть D=(V, X) – орграф, v
V, V1
V. Обозначим D(v)={wV| (v, w) X} – образ вершины v; D-1(v)={wV| (w,v) X} – прообраз вершины v; 
- образ множества вершин V1; 
- прообраз множества вершин V1. Пусть G=(V, X) – граф, vV, V1V. Обозначим G(v)={wV|{v, w}X} – образ вершины v; 
- образ множества вершин V1.
Пусть D=(V, X) – орграф с n 
2 вершинами и v, w – заданные вершины из V, где v w. Опишем алгоритм поиска кратчайшего пути из v в w в орграфе D.
Алгоритм Фронта Волны
Шаг 1. Помечаем вершину v индексом 0. Затем помечаем вершины, принадлежащие образу вершины v, индексом 1. Множество вершин с индексом 1 обозначаем FW1(v). Полагаем k=1.
Шаг 2. Если FWk(v)=
или выполняется k=n-1, w
FWk(v), то вершина w не достижима из v, и работа алгоритма на этом заканчивается. В противном случае переходим к шагу 3.
Шаг 3. Если wFWk(v), то переходим к шагу 4. В противном случае существует путь из v в w длины k, и этот путь является кратчайшим. Последовательность вершин
vw1w2…wk-1w,
где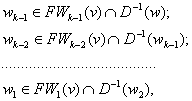 
и есть искомый кратчайший путь из v и w. На этом работа алгоритма заканчивается.
Шаг 4. Помечаем индексом k+1 все непомеченные вершины, которые принадлежат образу множества вершин с индексом k. Множество вершин с индексом k+1 обозначаем FWk+1(v). Присваиваем k:=k+1 и переходим к шагу 2.
Замечание. Множество FWk(v) обычно называют фронтом волны k-го уровня.
Замечание. Вершины w1w2…wk-1 , вообще говоря, могут быть выделены неоднозначно. Эта неоднозначность соответствует случаям, когда существует несколько различных кратчайших путей из v и w.
Пример 81.
Определить кратчайший путь из v1 и v6 в орграфе D, заданном матрицей смежности (табл. 3.2).
Таблица 3.2 Матрица смежности орграфа для примера 81
|
|
v1 |
v2 |
v3 |
v4 |
v5 |
v6 |
|
v1 |
0 |
0 |
0 |
1 |
1 |
0 |
|
v2 |
1 |
0 |
0 |
1 |
1 |
1 |
|
v3 |
1 |
1 |
0 |
1 |
1 |
1 |
|
v4 |
0 |
1 |
1 |
0 |
1 |
0 |
|
v5 |
1 |
1 |
1 |
1 |
0 |
0 |
|
v6 |
1 |
1 |
1 |
1 |
1 |
0 |
Решение.
Согласно алгоритму Фронта Волны, последовательно определяем
FW1(v1) = {v4, v5};
FW2(v1) = D(FW1(v1)){v1, v4, v5} = {v2, v3};
FW3(v1) = D(FW2(v1)){v1, v2, v3, v4, v5} = {v6}.
Таким образом, v6 Î FW3(v1), а значит, существует путь из v1 в v6 длины 3, и этот путь является кратчайшим. Найдем теперь кратчайший путь из v1 в v6. Определим множество
Выберем любую вершину из найденного множества, например вершину v3. Определим далее множество
Выберем любую вершину из найденного множества, например вершину v5. Тогда v1v5v3v6 – искомый кратчайший путь из v1 в v6 (длины 3) в орграфе D.