Классической в теории графов является следующая задача. В городе Кенигсберге имеется два острова, соединенных семью мостами с берегами реки Преголь и друг с другом так, как показано на рис. 3.18. Задача состоит в следующем: осуществить прогулку по городу таким образом, чтобы, пройдя по одному разу по каждому мосту, вернуться обратно. Решение этой задачи сводится к нахождению некоторого специального маршрута в графе.

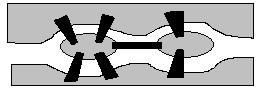
Рис. 3.18. Иллюстрация к классической задаче в теории графов

Пусть G – псевдограф.

Определение. Цепь (цикл) в G называется эйлеровой (эйлеровым), если она (он) проходит по одному разу через каждое ребро псевдографа G.

Поставим в соответствие схеме мультиграф G, изображенный на рис. 3.19, в котором каждой части суши соответствует вершина, а каждому мосту – ребро, соединяющее соответствующие вершины. На языке теории графов задача звучит следующим образом: найти эйлеров цикл в мультиграфе G.

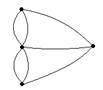
Рис. 3.19. Мультиграф к классической задаче о мостах

Определение. Граф является эйлеровым, если он содержит эйлеров цикл.

Рассмотрим вопрос о наличии эйлеровой цепи и цикла в псевдографе.

Теорема. Связный граф является эйлеровым тогда и только тогда, когда каждая вершина имеет четную локальную степень.

Теорема. Связный граф содержит  эйлерову цепь тогда и только тогда, когда ровно две вершины  имеют нечетную локальную степень.

Завершая рассмотрение эйлеровых графов, рассмотрим алгоритм построения эйлеровой цепи в данном эйлеровом графе. Этот метод известен под названием алгоритма Флёри.

Теорема. Пусть G – эйлеров граф; тогда следующая процедура всегда возможна и приводит к эйлеровой цепи графа G. Выходя из произвольной вершины и, идем по ребрам графа произвольным образом, соблюдая лишь следующие правила:

а) стираем ребра по мере их прохождения и стираем также изолированные вершины, которые при этом образуются;

б) на каждом этапе идем по мосту только тогда, когда нет других возможностей.

Пример 84.

Любой простой полный граф с нечетным количеством вершин является эйлеровым. Любой циклический граф является эйлеровым. Граф, являющийся колесом, не является эйлеровым.