Экспоненциальный закон

При экспоненциальном законе распреде­ления времени возникновения отказов интенсивность отказов является ве­личиной постоянной. Зависимости между основными количественными характери­стиками надежности будут выражены формулами:

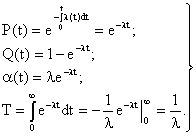                                                                   ^(3.1)

Основные количественные характеристики надежности для экспонен­циального закона приведены на рис. 3.1. Условие λ(f) = const означат, что средняя частота отказов и среднее время между соседними отказами соответственно равны интенсивности отказов и среднему времени безотказной работы аппаратуры, т.е.:

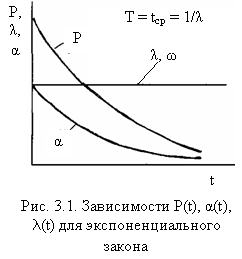
              (3.2)

Для экспоненциального закона распределения времени возникновения отказов средняя частота отказов превращается в интенсивность отказов, а среднее время между соседними отказами  –  в среднее время безотказной ра­боты. Основными же характеристиками надежности являются:

1) вероятность безотказной работы P(t);

2) интенсивность отказов l(t);

3) частота отказов α(t);

4) среднее время безотказной работы Т.

В случае экспоненциального закона эти характеристики пригодны для оценки надежности как аппаратуры разового использования, так и аппара­туры длительного использования, работающей в режиме смены отказавших элементов.

Из выражения для вероятности безотказной работы (3.1) видно, что она уменьшается с течением времени по экспоненциальному закону. Выражение

 

часто называют экспоненциальным законом надежности.

Выясним смысл среднего времени безотказной работы. Очевидно, что при t = Т вероятность безотказной работы будет иметь значение:

.

Из этого выражения видно, что при экспоненциальном законе надеж­ности среднее время безотказной работы – это время, в течение которого ве­роятность безотказной работы уменьшается в е раз.

Коэффициенты надежности для экспоненциального закона распреде­ления выражаются следующими формулами:

коэффициент готовности

;

коэффициент вынужденного простоя

;

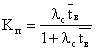коэффициент профилактики

;

частота профилактики

;

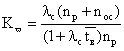коэффициент отказов элементов

;

относительный коэффициент отказов элементов

;

коэффициент расхода элементов

.

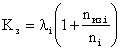Здесь l_c – интенсивность отказов системы, а l_i – интенсив­ность отказов элементов. Эти выражения становятся очевидными, если учесть, что в данном случае средняя частота отказов равна интенсивности отказов и        .

Выясним физический смысл коэффициентов, учитывающих вынуж­денный простой аппаратуры, для чего вычислим вероятность того, что в любой момент времени аппаратура будет исправна, если потоки отказов и восстановления простейшие.

Рассмотрим вначале промежуток времени от t до t + Dt, и вычислим вероятность того, что в конце этого промежутка аппаратура будет исправна.

Обозначим:

P(t + Dt) – вероятность того, что в конце промежутка t + Dt аппаратура будет исправна;

P(t) – вероятность того, что в момент времени t аппаратура будет исправна;

P₁(t) – вероятность того, что в момент времени t аппаратура находится в состоянии ремонта;

l – интенсивность отказов;

m_в – интенсивность восстановления.

Очевидно, что в конце промежутка Δt в силу ординарности потока отказов система будет исправна при следующих условиях:

а) в момент времени t аппаратура будет исправна и за промежуток Dt отказов не возникло;

б) в момент времени t аппаратура находилась в ремонте, но в течение Dt была восстановлена.

Предполагая, что промежуток времени Δt мал и ограничиваясь первыми двумя членами разложения показательной функции в ряд, можно для вероятностей событий а и б записать:

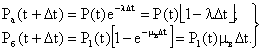                               (3.3)

Тогда вероятность безотказной работы аппаратуры на основании теоремы о полной вероятности будет:

или после очевидных преобразований

.

Устремляя Δt к нулю и переходя к пределу, получим:

.                                                  (3.4)

Так как состояния а и б образуют полную группу несовместимых событий, то

P_i(t) = l – P(t).

Подставляя это значение в формулу (3.4), получим:

                                             (3.5)

Предполагая, что при t = 0 система исправна, будем иметь Р(0) = 1, P₁(0) = 0. При этих начальных условиях решение дифференциального уравнения (3.5) имеет вид:

                                                  (3.6)

Учитывая, что

,

получим

.                                       (3.7)

Выражение (3.7) позволяет уяснить физический смысл коэффициентов К_г, К_п, К_пр.

Из выражения (3.7) видно, что при t = 0     P(t) = l, а при t = ∞   P(t) = K_г. Отсюда следует, что коэффициент готовности показывает вероятность исправного состояния системы в любой момент времени t при установившихся условиях эксплуатации. В начале же эксплуатации P(t) < K_r даже при простейших потоках отказов и восстановления.

Закон Рэлея

При распределении времени возникновения отказов по закону Рэлея частота отказов определяется из выражения:

                                                      (3.8)

где а – параметр распределения Рэлея.

Тогда вероятность безотказной работы, опасность отказов и среднее время безотказной работы будут выражаться следующими формулами:

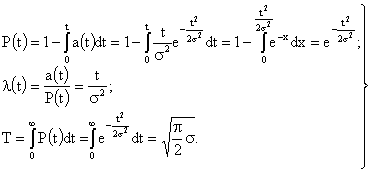;                             (3.9)

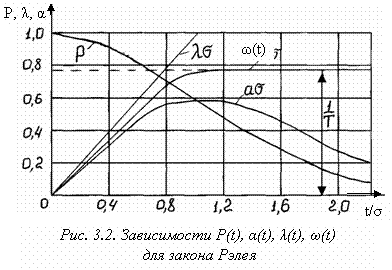
Зависимости основных количественных характеристик надежности для закона Рэлея приведены на рис. 3.2.

Из формул (3.9) видно, что интенсивность отказов растет линейно с течением времени. Это означает, что при распределении времени возникновения отказов по закону Рэлея происходит интенсивное старение аппаратуры, и количество отказов не удовлетворяет условиям стационарного случайного процесса. При этом с течением времени вероятность безотказной работы уменьшается значительно интенсивнее, чем при экспоненциальном законе.

Из выражения (3.9) для P(t) и рис. 3.2. также видно, что в области малых t  интенсивность безотказной работы системы уменьшается с течением времени медленнее, чем при экспоненциальном законе. Это означает, что сложные автоматические системы, предназначенные для малого времени непрерывной работы, целесообразно строить на элементах, имеющих рэлеевский закон распределения между отказами. Условие целесообразности применения таких элементов по сравнению с элементами, поток отказов которых подчиняется экспоненциальному распределению, аналитически можно записать в виде следующего неравенства:

.                                                     (3.10)

Это условие вытекает из сравнения выражений для вероятности безотказной работы при указанных законах распределения времени возникновения отказов.

В области больших значений t вероятность безотказной работы систе­мы с рэлеевским законом распределения уменьшается с течением времени значительно быстрее, чем при экспоненциальном. Это означает, что сконст­руировать на данных элементах высоконадежную систему, предназначен­ную для длительной непрерывной работы, затруднительно.

Найти аналитическое выражение для средней частоты отказов при распределении времени возникновения отказов по закону Рэлея весьма сложно. Поэтому оценим α(t) приближенно.

Так как Р(t) является возрастающей функцией, то средняя частота от­казов располагается между интенсивностью отказов l(t) и частотой отказов α(t). Кроме того,

l(0) = α(0) = w(0) =0.

В области больших значений t средняя частота отказов асимптотиче­ски стремится к среднему времени безотказной работы, т.е.:

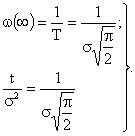                                              (3.11)

Тогда значение t, при котором происходит излом, будет равно:

.

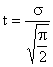Предполагая, что средняя частота представляет собой ломаную, сов­падающую в области малых значений t с интенсивностью отказов, а в облас­ти больших значений t с прямой α(t), можно записать:

 

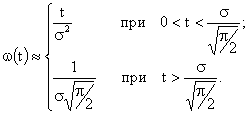
Зависимость  w(t) приведена на рис. 3.2. Коэффициенты надежности для случаев:

              и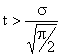                    

приближенно могут быть выражены соответственно формулами:

коэффициент готовности

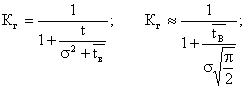
коэффициент вынужденного простоя

;

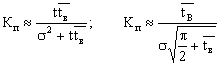коэффициент профилактики

;

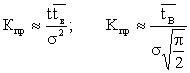частота профилактики

коэффициент отказов элементов

;

относительный коэффициент отказов элементов

;

коэффициент расхода элементов

.

Здесь s_с – параметр распределения отказов системы, s_i – параметр распределения отказов элементов.

Из выражений для коэффициентов надежности видно, что в данном случае они являются функциями времени. Исключение составляют лишь ко­эффициенты отказов элементов.

Нормальное распределение

Длительность безотказной работы аппа­ратуры не может быть отрицательной. Поэтому количественные характери­стики надежности имеет смысл рассматривать только при усеченном нор­мальном законе распределения времени между отказами.

Частота отказов в этом случае определяется из выражения:

.                                                (3.12)

Здесь T₁, s² – среднее значение и дисперсия времени между отказами в нормальном законе соответственно, С  –  постоянная усеченного нормального распределения, которая выбирается из условия:

,

и равна

.

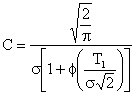Тогда вероятность безотказной работы можно представить в виде:

                                         (3.13)

где 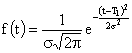 – нормальный закон распределения времени между отказами.

Подставляя в выражение (3.13) значение постоянной С и вычисленный интеграл, получим следующую формулу для вероятности безотказной ра­боты:

.

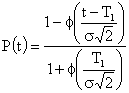Интенсивность отказов в данном случае будет равна:

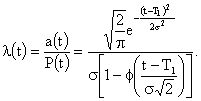                                       (3.15)

Вычислим среднее время безотказной работы. Для рассматриваемого случая:

.

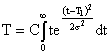Обозначим:

,

тогда

.

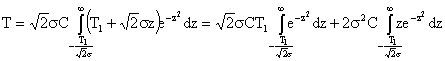Вычислим первый интеграл вероятности, пользуясь известным соотношением:

,

тогда получим:

.

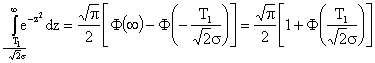Второй интеграл будет иметь вид:

.

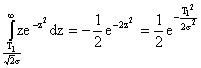Подставляя вычисленные интегралы в выражение для Т и делая элементарные преобразования, получим выражение среднего времени безотказной работы в виде:

.

Основные характеристики надежности для нормального закона распределения между отказами имеют вид (рис. 3.3).

Из рисунка 3.3 видно, что интенсивность отказов начинается с нуля и с течением времени сильно растет. Это означает, что поток отказов не является стационарным и происходит старение элементов. В области малых значений t старение элементов оказывает несущественное влияние на надежность, и поэтому вероятность безотказной работы системы уменьшается незначительно. При длительной эксплуатации системы, отказы элементов которой имеют нормальное распределение, ее надежность быстро снижается, и поэтому вероятность безотказной работы быстро падает.

Гамма-распределение

При этом распределении частота отказов выражается формулой:

,                                                (3.16)

где l₀ – параметр гамма-распределения.

Тогда при целом и положи­тельном k вероятность безотказной работы, опасность отказов и среднее время безотказной работы выражается следующими формулами:

                  (3.17)

Параметр гамма-распределения характеризует асимметрию и эксцесс гамма-распределе­ния. В зависимости от его значения существенно изменится вид основных количественных характеристик надёжности. Зависимости a(t), l(t) и P(t) приведены на рис. 3.4. Из рисунка и выражения (3.16) видно, что при k = l гамма-распределение превращается в экспоненциальное. При k > l интенсивность отказов возрастает, а при k < l убывает.

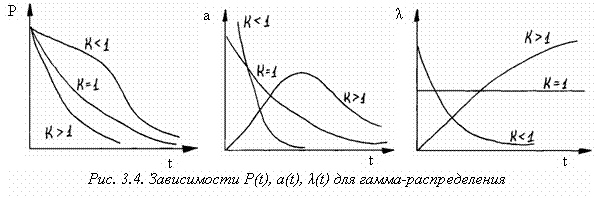Гамма-распределению удовлетворяет время возникновения отказов резервированных систем с включением резерва по способу замещения и при условии, что потоки отказов основной системы и всех резервных являются простейшими. В этом случае параметр распределения k равен числу всех систем (основной и резервных), т.е.

k = m + l.

Гамма-распределение также может быть характеристикой времени возникновения отказов сложных электромеханических систем, если имеют место мгновенные отказы элементов на начальной стадии эксплуатации или в процессе обработки системы, т.е. при k < l гамма-распределение является удобной характеристикой времени возникновения отказов аппаратуры в течение времени её приработки.

Распределение Вейбулла

При распределении Вейбулла частота отказов задается выражением:

.                                              (3.18)

Параметр l₀ определяет масштаб, а параметр k – асимметрию и эксцесс распределения. Для распределения Вейбулла основные количественные характеристики надёжности выражаются следующими формулами:

;

;

.

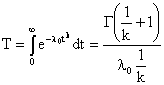Зависимости основных количественных характеристик надёж­ности от времени приведены на рис. 3.5. Из рисунков и выражения (3.18) видно, что при k = l распределение Вейбулла превращается в экспо­ненциальное распределение. При k > l интенсивность отказов начина­ется с нуля и с течением времени возрастает. При k < l интенсивность отказов начинается с +∞ и в области больших t стремится к нулю.

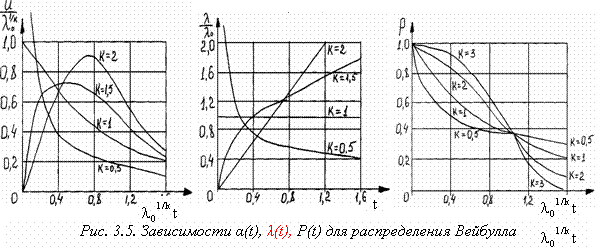Это означает, что распределение Вейбулла так же, как и гамма-распределение, по-видимому, может быть использовано в качестве характеристики надёжности ап­паратуры в течение времени её приработки. Это распределение на­блюдается для некоторых механических деталей и, в частности, при­меняется при изучении надёжности шарикоподшипников. Распределение Вейбулла с параметром k = 1,4 – 1,9 наблюдается у неко­торых типов электронных ламп. Оно также может быть использовано при ускоренных испытаниях элементов в форсированных режимах.

Для распределения Вейбулла так же, как и для гамма-распределения, не удаётся в общем виде найти выражение для средней частоты отказов, что затрудняет анализ системы по коэффициентам надёжности, так как приходится решать интегральное уравнение Вольтерра приближенными способами.

Суперпозиция распределений

Рассмотренные законы распределения времени возникновения отказов могут в большинстве случаев характеризовать надёжность сложной системы лишь на ограниченных участках времени её работы. Так, например, на участке приработки время возникновения отказов может подчиняться гамма-распределению или распределению Вейбулла, на участке нормальной работы – экспоненциальному, а на участке старения – нормальному распределению. В связи с этим для оценки надёжности сложной систе­мы на длительном участке её эксплуатации целесообразно использо­вать суперпозицию рассмотренных законов распределения времени между отказами.

В качестве примера рассмотрим суперпозицию двух экспонен­циальных законов.

Пусть

,

где l₁ < l₂, C₁, C₂ – постоянные, определяемые из условия С₁ + С₂ = 1 и зависящие от соотношения между l₁ и l₂.

Для этого случая основные количественные характеристики надежности будут иметь вид:

;

;

.

Так как l₂ > l₁, то в области больших значений t члены в выраже­нии для интенсивности отказов, имеющие множителем е^-l2t, близки к нулю и тогда l(t) » l₁. При малых значениях t            e^-l1t        и         е^-l2t близки к единице, и

l(t) = C₁l₁ + C₂l₂ > l₁.

Таким образом, интенсивность отказов с течением времени уменьшается:

от          l(t) =C₁l₁ + C₂l₂       при t = 0

до          l₁                                при t ® ∞.

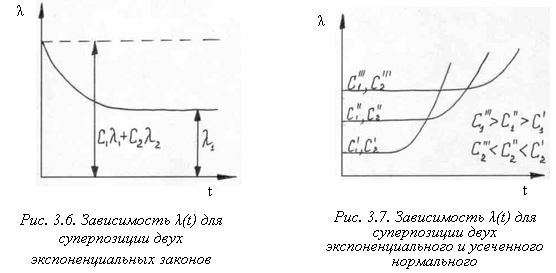Зависимость l(t) для суперпозиции двух экспоненциальных за­конов при l₂ < l₁ показана на рисунке (3.6.). На рисунке видно, что за­кон распределения, представляющий собой суперпозицию двух экспоненциальных законов, может характеризовать на

дёжность сложной системы с учётом периода приработки. Такой же вывод можно было бы получить при суперпозиции экспоненциального закона с гамма-распределением и распределением Вейбулла при k < l .

Влияние постепенных отказов может быть уточнено при суперпозиции экспоненциального и усеченного нормального законов распределения. В этом случае частота отказов представляется в следующем виде:

,

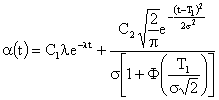где С₁ и С₂ – коэффициенты, учитывающие степень влияния внезапных и постепенных отказов.

Тогда основные количественные характеристики надёжности можно представить в виде следующих соотношений:

;

.

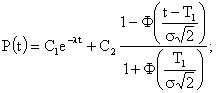
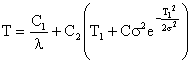Зависимость λ(t) для различных С₁и С₂ показаны на рис. (3.7.). Из рисунка видно, что в области малых значений t интенсивность от­казов – величина постоянная, а в области больших t она возрастает, что свидетельствует о появлении старения аппаратуры и, как следст­вие, возникновении постепенных отказов.