Алгебраический критерий устойчивости Шур-Кона позволяет анализировать устойчивость замкнутых дискретных САУ по их характеристическому уравнению, записанному в z-изображениях:

.

Для оценки устойчивости системы определяются знаки у k определителей  размерностью , где i необходимо изменять от 1 до k:

Каждый из этих определителей состоит из четырех подопределителей размерностью , которые заполняются коэффициентами характеристического уравнения по следующим правилам. Элементы главных диагоналей первого и четвертого подопределителей равны коэффициенту , а второго и третьего – коэффициенту .

Далее каждый из подопределителей заполняется по столбцам, начиная от коэффициента находящегося на его главной диагонали. При этом индексы коэффициентов в первом и во втором подопределителях с увеличением номера строки последовательно возрастают, а в третьем и четвертом подопределителях – убывают. Когда значение индекса коэффициента достигает 0 или , дальнейшее заполнение столбца производится нулями.

Для устойчивости дискретной системы необходимо и достаточно, чтобы определители  при четном i были положительны, а при нечетном i – отрицательны. При первом же нарушении указанного правила, выявленном в процессе изменения i от 1 до k, можно сделать заключение о неустойчивости системы.

Пример 19

Необходимо оценить устойчивость замкнутой дискретной САУ, рассмотренной в примере 18.

Ее характеристическое уравнение:

.

При i = 1:

Поскольку сформулированные условия на первом этапе оценки устойчивости не нарушены, необходимо перейти к составлению и вычислению определителя, соответствующего i = 2:

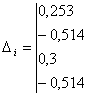
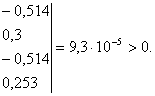
Как и следовало ожидать, повторная проверка устойчивости рассматриваемой системы дает тот же результат – система устойчива. Очевидно, что для этой системы проще оценивать устойчивость по расположению корней характеристического уравнения. Но для систем более высокого порядка использование критерия Шур-Кона может быть эффективным, поскольку задача составления определителей  при их кажущейся громозкости легко формализуется и решается с использованием ЭВМ.