Математические модели на основе систем обыкновенных дифференциальных уравнений (ОДУ) записываются либо в нормальной форме Коши (3.8), либо в неявной форме ОДУ (3.9):
; (3.8)
(3.9)
где U – вектор переменных состояния моделируемого объекта, 
- вектор производных переменных состояния по времени, t – время (начальные условия U0 = U|t=0), F – вектор-функция.
Система (3.8) является частным случаем (3.9), если последнюю удается разрешить относительно вектора U.
Анализ переходных процессов сводится к численному интегрированию (3.8) или (3.9) /4/. Все численные методы интегрирования ОДУ основаны на последовательном нахождении значений U, начиная с U0, то есть U0, U1, U2, …, Um. Таким образом, решение задачи сводится к нахождению для каждого очередного момента времени ti+1 значений Ui+1, согласно формуле 
, где G – некоторая функция, определяемая методом решения.
Основные требования, предъявляемые к методу интегрирования ОДУ в САПР, АРМ:
- универсальность, то есть применимость к анализу любого объекта из данного класса объектов проектирования;
- алгоритмическая надежность;
- достаточная точность результатов;
- умеренные затраты ресурсов ЭВМ (памяти и машинного времени).
Основные характеристики методов интегрирования, от которых зависит их эффективность, — это точность и устойчивость методов, а также связанная с ними стратегия выбора величины шага интегрирования.
Приведем пример решения ОДУ, описывающего динамику управляющего гидроустройства.
Пример 4. Во многих машинах (плоскошлифовальные станки, промышленные роботы и др.) масса, приведенная к поршню гидроцилиндра, изменяется в широких пределах. Известно, что для повышения точности обработки (или позиционирования) и уменьшения длительности цикла подобных машин должен быть ограничен модуль ускорения, а продолжительность и путь выбега должны быть снижены до разумных пределов.
На рис. 3.6 представлена схема рабочей части гидропривода, состоящей из силового гидроцилиндра (Ц), источника питания (И), состоящего из нерегулируемого насоса и переливного клапана /11/. Установившаяся скорость поршня (П) настраивается с помощью дросселя (Д) с ручным управлением. Направление движения поршня и его остановка определяются положением золотника трехпозиционного распределителя (Р). Для обеспечения при выбеге необходимых условий и законов движения служит управляющее гидроустройство (УГ) с гидравлическим управлением. Скорость золотника УГ настраивается дросселями с обратными клапанами.
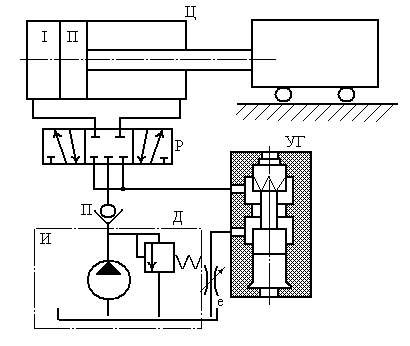
Рис. 3.6. Схема рабочей части гидропривода
Уравнение движения подвижного элемента гидропривода получено в работе / 11/ и имеет вид ОДУ в нормальной форме Коши (3.8):
,
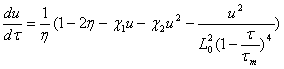где u – безразмерная скорость поршня; τ – безразмерное время; η – коэффициент, зависящий от приведенной к поршню гидроцилиндра массы, постоянного модуля ускорения, масштабного коэффициента напряжения и коэффициента площади штока; χ1, χ2 и L0 – коэффициенты; τm – безразмерное время выбега.
Безразмерные коэффициенты χ1, χ2, L0 и τm являются постоянными и связаны с параметрами модели. Диапазон изменения коэффициентов ограничен: 0≤η≤½¸ 0< χ1<½, 0< χ2<¼. Искомой функцией является безразмерная скорость поршня в функции от безразмерного времени u(τ).
Решение ОДУ возможно различными способами в различных вычислительных средах, однако приведем решение в среде MathCAD:
Константы моделирования:
n:=50
Решение дифференциального уравнения:
;
.
Используем формулу дифференцирования назад:
.
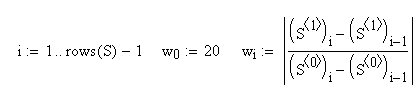Для интегрирования используем составную квадратурную формулу прямоугольников:
.
На рис. 3.7 представлена диаграмма безразмерных коэффициентов перемещений, скоростей и ускорений поршня гидроустройства. Здесь все константы заданы в безразмерном виде в начале модели, и через них можно определить геометрические, массовые и другие параметры управляющего гидроустройства.
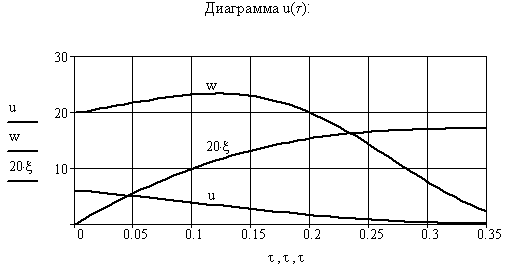
Рис. 3.7. Диаграммы ξ(τ), u(τ) и w(τ).
Решение дифференциального уравнения получено с помощью встроенной функции rkfixed(), в результате чего найдена искомая функция u(τ). Дифференцирование функции u(τ) дает возможность найти безразмерное ускорение поршня w(τ), для чего использована формула дифференцирования назад. Для определения безразмерного перемещения поршня ξ(τ) использована составная квадратичная формула прямоугольников.
Таким образом, с помощью представленной модели, реализованной как фрагмент АРМ, осуществляется моделирование переходных процессов и подбор параметров управляющего гидроустройства, то есть решается задача проектирования описанного объекта.
Моделирование статических режимов
Для большинства проектируемых динамических объектов переходные процессы носят асимптотически устойчивый характер, то есть при t → ∞ объект переходит в определенное устойчивое состояние. В связи с этим важной задачей одновариантного анализа в САПР, АРМ является расчет параметров модели в устойчивом состоянии, то есть расчет статического режима объекта.
В статическом режиме производные выходных параметров по времени равны нулю и отсутствуют меняющиеся во времени внешние воздействия, поэтому ММ статических состояний можно определить непосредственно из ММ динамических процессов (3.8) или (3.9). В результате получаются системы АУ относительно соответствующих переменных:
F(U,t) = 0 или Ф(U,t) = 0.
Таким образом, одновариантный анализ статических режимов физических объектов, описываемых системой ОДУ, сводится к решению системы АУ общего вида
F(X) = 0, (3.10)
где Х – вектор неизвестных параметров. В работах /8,10/ студенты специальности 2204 достаточно подробно знакомятся с численными методами решения систем АУ. В САПР применяют в основном методы простой итерации, Ньютона и релаксационные. Методы простой итерации и релаксационные имеют линейную скорость сходимости и требуют небольших вычислительных затрат на одну итерацию. Эти методы применяются в основном для решения систем АУ большой размерности. Метод Ньютона имеет квадратичную скорость сходимости, но в общем случае сходится только в окрестности точного решения. На рис. 3.8 показан пример решения нелинейного алгебраического уравнения встроенными средствами MathCAD и функцией пользователя N(), реализованной методом Ньютона.
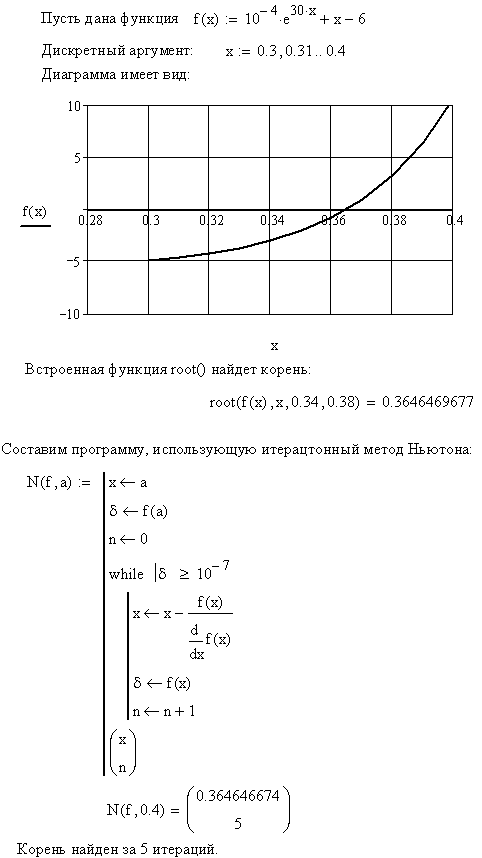
Рис. 3.8. Пример решения нелинейного АУ в системе MathCAD